Когда бросается монета, можно сказать, что она упадет орлом вверх, или вероятность этого составляет 1/2. Конечно, это не означает того, что если монета подбрасывается 10 раз, она обязательно упадет вверх орлом 5 раз. Если монета является «честной» и если она подбрасывается много раз, то орел выпадет очень близко в половине случаев. Таким образом, существует два вида вероятностей: экспериментальная и теоретическая.
Экспериментальная и теоретическая вероятность
Если бросить монетку большое количество раз — скажем, 1000 — и посчитать, сколько раз выпадет орел, мы можем определить вероятность того, что выпадет орел. Если орел выпадет 503 раза, мы можем посчитать вероятность его выпадения:
503/1000, или 0,503.
Это экспериментальное определение вероятности. Такое определение вероятности вытекает из наблюдения и изучения данных и является довольно распространенным и очень полезным. Вот, к примеру, некоторые вероятности которые были определены экспериментально:
1. Вероятность того, что у женщины разовьется рак молочной железы составляет 1/11.
2. Если вы целуетесь, с кем-то, кто болен простудой, то вероятность того, что вы тоже заболеете простудой, составляет 0,07.
3. Человек, который только что был освобожден из тюрьмы, имеет 80% вероятности возвращения назад в тюрьму.
Если мы рассматриваем бросание монеты и беря во внимание то, что столь же вероятно, что выпадет орел или решка, мы можем вычислить вероятность выпадение орла: 1 / 2. Это теоретическое определение вероятности. Вот некоторые другие вероятности, которые были определены теоретически, с помощью математики:
1. Если находится 30 человек в комнате, вероятность того, что двое из них имеют одинаковый день рождения (исключая год), составляет 0,706.
2. Во время поездки, Вы встречаете кого-то, и в течение разговора обнаруживаете, что у вас есть общий знакомый. Типичная реакция: «Этого не может быть!». На самом деле, эта фраза не подходит, потому что вероятность такого события достаточно высока — чуть более 22%.
Таким образом, экспериментальная вероятность определяются путем наблюдения и сбора данных. Теоретические вероятности определяются путем математических рассуждений. Примеры экспериментальных и теоретических вероятностей, как например, рассмотренных выше, и особенно тех, которые мы не ожидаем, приводят нас, к ваэности изучения вероятности.
Вы можете спросить: «Что такое истинная вероятность?» На самом деле, таковой нет. Экспериментально можно определить вероятности в определенных пределах. Они могут совпадать или не совпадать с вероятностями, которые мы получаем теоретически. Есть ситуации, в которых гораздо легче определить один из типов вероятности, чем другой. Например, было бы довольно найти вероятность простудиться, используя теоретическую вероятность.
Вычисление экспериментальных вероятностей
Рассмотрим сначала экспериментальное определение вероятности. Основной принцип, который мы используем для вычисления таких вероятностей, является следующим.
Принцип P (экспериментальный)
Если в опыте, в котором проводится n наблюдений, ситуация или событие Е происходит m раз за n наблюдений, то говорят, что экспериментальная вероятность события равна P (E) = m/n.
Пример 1 Социологический опрос. Было проведено экспериментальное исследование, чтобы определить количество левшей, правшей и людей, у которых обе руки развиты одинаково Результаты показаны на графике.
a) Определите вероятность того, что человек — правша.
b) Определите вероятность того, что человек — левша.
c) Определите вероятность того, что человек одинаково свободно владеет обеими руками.
d) В большинстве турниров, проводимых Профессиональной Ассоциацией Боулинга, участвуют 120 игроков. На основании данных этого эксперимента, сколько игроков могут быть левшой?
a)Число людей, являющиеся правшами, составляет 82, количество левшей составляет 17, а число тех, кто одинаково свободно владеет двумя руками — 1. Общее количество наблюдений — 100. Таким образом, вероятность того, что человек правша, есть Р
P = 82/100, или 0,82, или 82%.
b) Вероятность того, что человек левша, есть Р, где
P = 17/100, или 0,17, или 17%.
c) Вероятность того, что человек одинаково свободно владеет двумя руками составляет P, где
P = 1/100, или 0,01, или 1%.
d) 120 игроков в боулинг, и из (b) мы можем ожидать, что 17% — левши. Отсюда
17% от 120 = 0,17.120 = 20,4,
то есть мы можем ожидать, что около 20 игроков являются левшами.
Пример 2 Контроль качества. Для производителя очень важно держать качество своей продукции на высоком уровне. На самом деле, компании нанимают инспекторов контроля качества для обеспечения этого процесса. Целью является выпуск минимально возможного количества дефектных изделий.
Но так как компания производит тысячи изделий каждый день, она не может позволить себе проверять каждое изделие, чтобы определить, бракованное оно или нет. Чтобы выяснить, какой процент продукции являются дефектным, компания проверяет гораздо меньше изделий.
Министерство сельского хозяйства США требует, чтобы 80% семян, которые продают производители, прорастали. Для определения качества семян, которые производит сельхозкомпания, высаживается 500 семян из тех, которые были произведены. После этого подсчитали, что 417 семян проросло.
a) Какова вероятность того, что семя прорастет?
b) Отвечают ли семена государственным стандартам?
Решение a) Мы знаем, что из 500 семян, которые были высажены, 417 проросли. Вероятность прорастания семян Р, и
P = 417/500 = 0,834, или 83.4%.
b) Так как процент проросших семян превысил 80% по требованию, семена отвечают государственным стандартам.
Пример 3 Телевизионные рейтинги. Согласно статистических данных, в Соединенных Штатах 105 500 000 домохозяйств с телевизорами. Каждую неделю, информация о просмотре передач собирается и обрабатывается. В течение одной недели 7815000 домохозяйств были настроены на популярный комедийный сериал «Все любят Реймонда» на CBS и 8302000 домохозяйств были настроены на популярный сериал «Закон и порядок» на NBC (Источник: Nielsen Media Research). Какова вероятность того, что телевизор одного дома настроен на «Everybody Loves Raymond» в течение данной недели? на «Закон и порядок»?
Решениеn Вероятность того, что телевизор в одном домохозяйстве настроен на «Все любят Реймонда» равна Р, и
P = 7,815,000/105,500,000 ≈ 0,074 ≈ 7,4%.
Возможность, что телевизор домохозяйства был настроен на «Закон и порядок» составляет P, и
P = 8,302,000/105,500,000 ≈ 0,079 ≈ 7,9%.
Эти проценты называются рейтингами.
Теоретическая вероятность
Предположим, что мы проводим эксперимент, такие, как бросание монетки ли дротиков, вытаскивание карты из колоды, или проверка изделий на качество на сборочной линии. Каждый возможный результат такого эксперимента называется исход. Множество всех возможных исходов называется пространством исходов. Событие это множество исходов, то есть подмножество пространства исходов.
Пример 4 Бросание дротиков. Предположим, что в эксперименте «метание дротиков» дротик попадает в мишень. Найдите каждое из нижеследующих:
b) Пространство исходов
Решение
a) Исходы это: попадание в черное (Ч), попадание в красное (К) и попадание в белое (Б).
b) Пространство исходов есть , которое может быть записано просто как .
Пример 5 Бросание игральных костей. Игральная кость это куб с шестью гранями, на каждой их которых нарисовано от одной до шести точек.
Предположим, что мы бросаем игральную кость. Найдите
a) Исходы
b) Пространство исходов
Решение
a) Исходы: 1, 2, 3, 4, 5, 6.
b) Пространство исходов .
В случайном эксперименте симметричную монету..
1) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что оба раза выпадет орёл.
* Составим список возможных вариантов. Бросают 2 раза может выпасть О — Орел, Р — Решка:
ОО
ОР
РО
РР
Всего 4 исхода из них только один случай удовлетворяет условию.
* Вероятность(P) = 1 / 4 = 0.25
Ответ: 0.25
2) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что оба раза выпадет решка.
* Составим список возможных вариантов. Бросают 2 раза может выпасть О — Орел, Р — Решка:
ОО
ОР
РО
РР
Всего 4 исхода из них только один случай удовлетворяет условию, что оба раза выпадет решка.
* Вероятность(P) = 1 / 4 = 0.25
Ответ: 0.25
3) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что один раз выпадет орёл, а другой — решка.
* Составим список возможных вариантов. Бросают 2 раза может выпасть О — Орел, Р — Решка:
ОО
ОР
РО
РР
Всего 4 исхода из них только 2 случая удовлетворяют условию, что один раз выпадет орел, а другой раз решка.
* Вероятность(P) = 2 / 4 = 1 / 2 = 0.5
Ответ: 0.5
4) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.
* Составим список возможных вариантов. Бросают 2 раза может выпасть О — Орел, Р — Решка:
ОО
ОР
РО
РР
Всего 4 исхода из них только два удовлетворяют условию, что решка выпадет ровно 1 раз.
* Вероятность(P) = 2 / 4 = 0.5
Ответ: 0.5
5) В случайном эксперименте симметричную монету бросают дважды.Найдите вероятность того, что орёл выпадет чётное число раз.
* Составим список возможных вариантов. Бросают 2 раза может выпасть О — Орел, Р — Решка:
ОО
ОР
РО
РР
Всего 4 исхода из них один удовлетворяет условию, что Орел выпадет четное число раз.
* Вероятность(P) = 1 / 4 = 0.25
Ответ: 0.25
Источник: vopvet.ru
Вероятность с монетами как решать
Наши Партнеры:
- Еще немного про параболу
- ЕГЭ скоро….
- Еще немного.
Главная > Решебники > Чудесенко > Чудесенко. Теория вероятностей и математическая статистика. Задача 16.
Чудесенко. Теория вероятностей и математическая статистика. Задача 16.
16. Монета бросается до тех пор, пока герб не выпадет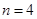 
раза. Определить вероятность того, что цифра выпадет 
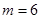раз.
Решение:
По условию задачи герб должен выпасть 4 раза, а решка – 6 раз, значит, всего бросков должно быть 10 штук.
Таким образом, требуется найти вероятность такого события, что из первых девяти бросков выпало 3 герба, и на 10-ый бросок также выпал герб.
Обозначим события:
А – «из 9 бросков выпало 3 герба»
В — «на 10-ый бросок выпал герб».
При этом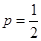 
— вероятность того, что при одном броске выпадет герб.
Для определения вероятности события А используем формулу Бернулли:
,
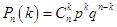где n – количество экспериментов, k – количество благоприятных исходов, p – вероятность благоприятного исхода. Подставим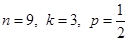 
.
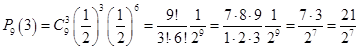
С вероятностью события В немного проще:
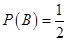
Тогда, по теоремам умножения и сложения вероятностей:
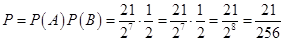
Ответ: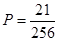 
Источник: kontromat.ru