Корреляция – статистическая взаимосвязь двух параметров между собой; сила этой взаимосвязи измеряется т.н. коэффициентом корреляции.
Коэффициент корреляции (r) – показывает, в какой степени значения одного параметра изменяются при пропорциональном изменении значений другого параметра. Проще говоря, коэффициент корреляции показывает, на какую величину изменится значение одного параметра при изменении значения другого параметра на единицу. Т.о., если коэффициент корреляции равен +0,85, то при изменении значения любого из параметров на +1 значение другого параметра также вырастет на 0,85; если же коэффициент корреляции равен –0,47, то при изменении величины любого из параметров на +1 значение другого параметра изменится на –0,47, т.е. уменьшится на 0,47. Величина коэффициента корреляции изменяется от –1 до +1, причем 0 означает отсутствие корреляции.
Если значение коэффициента корреляции положительное (больше нуля), такая корреляция называется прямой или положительной. Если значение коэффициента корреляции отрицательное (меньше нуля), то соответствующая корреляция называется обратной или отрицательной. Прямая корреляция означает, что при увеличении одного параметра другой также увеличивается, в случае обратной корреляции – соответственно, уменьшается.
Как для остальных видов статистического анализа, для корреляции рассчитывается показатель вероятности нулевой гипотезы (р), который должен быть равен или меньше заранее оговоренного уровня значимости (α) – см. раздел 8 настоящей главы. Обычно уровень значимости устанавливается равным 0,05 (что обычно для биомедицинских исследований), с возможным внесением поправки на проблему множественных сравнений (см. выше).
В зависимости от величины по модулю коэффициента корреляции сила корреляционной взаимосвязи классифицируется как:
| r | ≤ 0,25 – слабая корреляция;
| r | ≥ 0,75 – сильная корреляция.
Возможны ситуации, когда найденная корреляционная зависимость не может быть корректно учтена и использована при формулировке выводов исследования:
1. Корреляция статистически значима (р меньше или равен принятому уровню значимости, например, 0,05), но коэффициент корреляции слишком мал (≤0,25). Такие корреляции могут представлять интерес для исследователей неявных тенденций в больших популяциях, но для клиники они, как правило, не важны, поскольку описываемые ими взаимообусловленные изменения параметров организма слишком незначительны. Проще говоря, такая корреляция статистически значима, но клинически незначима. Подобные зависимости во множестве выявляются при анализе выборок большого размера. Обычно в клинических исследованиях принимают во внимание как минимум корреляции средней силы;
2. Коэффициент корреляции высок, но она статистически незначима (р>0,05 либо иного уровня значимости, принятого исследователями). Проще говоря, такая корреляция клинически значима, но статистически незначима. Подобные ситуации, как правило, имеют место при малом размере анализируемой выборки; при этом увеличение размера выборки до рекомендованного (см.
Главу III, раздел 6.5) может повысить статистическую значимость корреляции до приемлемой (в случае, если корреляционная зависимость действительно имеет место). Необходимо помнить о том, что в малых выборках высока вероятность выявления взаимосвязей, обусловленных исключительно случайным сочетанием значений параметров, причем чем меньше размер выборки, тем выше роль случайности в результатах статистической обработки. Как указывалось ранее, статистическая обработка данных, полученных при анализе выборок, включающих менее 20 наблюдений, почти всегда не имеет смысла.
Методы корреляционного анализа могут быть параметрическими (предназначенными для анализа взаимозависимости нормально распределенных данных) и непараметрическими.
Параметрический корреляционный анализ – Пирсона.
Критерии применимости корреляционного анализа Пирсона:
1. Все учитываемые признаки должны быть нормально распределены;
2. Все учитываемые признаки должны быть количественными.
Непараметрический корреляционный анализ – Спирмена, Тау Кендалла, Гамма.
Критерии применимости перечисленных разновидностей корреляционного анализа:
1. Учитываемые признаки – количественные, распределения которых не являются нормальными либо неизвестны (по крайней мере, для одного из признаков);
2. Возможен анализ смеси количественных и качественных (порядковых) признаков;
3. Возможен анализ нескольких качественных (порядковых) признаков.
Ранговая корреляция Спирмена (ρ) – универсальный метод, используется для оценки взаимосвязи количественных (независимо от вида распределения) и/или порядковых (качественных) признаков. Наиболее популярный метод корреляционного анализа.
Ранговая корреляция Тау Кендалла (τ) – используется для оценки взаимосвязи порядковых признаков или смеси количественных и порядковых признаков.
Гамма-корреляция (γ) – используется, когда в анализируемых переменных имеется много вариант, значения которых совпадают.
Как и для прочих статистических показателей, для коэффициента корреляции может быть рассчитан доверительный интервал. Вычисляется он следующим образом:
1. Вычисляется функция z:
Здесь r – коэффициент корреляции.
2. Вычисляется стандартная ошибка m для z:
Здесь n – количество наблюдений в переменных, для которых рассчитывается коэффициент корреляции.
3. Вычисляются нижний и верхний пределы функции z (z1 и z2):
Здесь t – значение t-критерия для данного числа степеней свободы (см. выше: df = n–1) и заданного уровня значимости α (обычно р≤0,05). Подсчет t-критерия обычно выполняется при помощи специальной функции программы статистической обработки. Например, в программах семейства Statistica этот подсчет реализован следующим образом (см. рис. 23):
 |
Рис. 23. Подсчет t-критерия Стьюдента для данного числа степеней свободы и заданного уровня значимости α, реализованный в программах Statistica 7.0 и 8.0.
4. Вычисляются нижний и верхний пределы ДИ для коэффициента корреляции r:
С вероятностью 95% истинное значение коэффициента корреляции, вычисленное на основе анализа генеральной совокупности, находится в указанных границах.
Коэффициенты корреляции можно попарно сравнивать. Для проверки гипотезы о равенстве двух корреляций (H0) величины сравниваемых коэффициентов корреляций r1 и r2 подвергаются z-преобразованию Фишера:
После этого вычисляется стандартная ошибка разницы по формуле:
n1 – количество пар значений переменных для первого коэффициента корреляции;
n2 – количество пар значений переменных для второго коэффициента корреляции.
Затем вычисляется значение t-критерия Стьюдента по формуле: t = (z1 – z2)/Sd
Для дальнейших расчетов берется абсолютное значение этого числа.
Затем вычисляется количество степеней свободы (df). В данном случае df = (n1 + n2) – 2
Зная t и df, при помощи таблицы критических значений t-критерия Стьюдента можно определить р (см. рис. 24).
 |
Рис. 24. Сокращенная таблица критических значений t-критерия Стьюдента. Здесь df – число степеней свободы, α – уровень значимости (в данном случае будет соответствовать р).
Можно также вычислить доверительные интервалы для обоих сравниваемых коэффициентов корреляции и посмотреть, не пересекаются ли они: если ДИ пересекаются (границы ДИ накладываются друг на друга), то коэффициенты корреляции значимо не различаются.
Вышеописанные вычисления можно быстро выполнить при помощи описанного ранее диалогового окна программы Statistica версий 7.0 и 8.0 (см. рис. 22). Для этого необходимо знать величины собственно сравниваемых коэффициентов корреляции, число наблюдений (n) для каждого из них, а также тип статистической гипотезы (направленная или ненаправленная, т.е. одно- или двусторонняя – см. выше).
Ведя речь о корреляционном анализе, необходимо указать, что нельзя слепо доверяться его результатам. Дело в том, что довольно простая формула, по которой рассчитывается коэффициент корреляции, ничего не знает о том, существует ли взаимосвязь между анализируемыми признаками в действительности – она лишь анализирует по ряду формальных критериев функции, описывающие изменение этих признаков, и сравнивает полученные результаты друг с другом.
Проще говоря, если два признака по чистой случайности изменяются сходным образом, они будут коррелировать между собой. Естественно, выявленные при помощи таких корреляций «взаимосвязи» пополняют копилку научных анекдотов. Так, на рис. 25 представлена взаимосвязь между количеством убийств в США и частотой использования браузера Internet Expolrer с очевидной сильной прямой корреляцией между указанными факторами, причем данные удивительным образом даже не подтасованы [4, 3].
Рис. 25. Взаимосвязь между количеством убийств в США и доли браузера Internet Explorer на рынке браузеров (данные за 2006-2011 гг.).
Еще один замечательный пример абсурдной корреляции показан на рис. 26, где отчетливо прослеживается взаимосвязь между количеством скачиваний известной свободной операционной системы Linux и количеством поисковых запросов по поводу прыщей (данные из кэша поисковых запросов портала Yandex).
В целом, выявление при анализе взаимосвязи неких факторов А и В статистически значимого коэффициента корреляции, соответствующего взаимозависимости средней силы и более, может свидетельствовать о том, что в реальности:
1. Признак А влияет на признак В;
2. Признак В влияет на признак А;
3. На оба признака влияет неизвестный третий фактор С;
4. Признаки А и В не влияют друг на друга, но по чистой случайности изменяются сходным образом (параллельно).
Рис. 26. Взаимосвязь между количеством скачиваний операционной системы Linux и количеством поисковых запросов по поводу прыщей (данные из кэша Yandex).
Таким образом, корреляционный анализ устанавливает наличие и силу только статистической связи, и наличие корреляции двух признаков (любой силы) не может интерпретироваться как доказательство причинно-следственной связи этих признаков.
Говоря о практической стороне дела, при анализе коэффициентов корреляции необходимо принимать во внимание следующие соображения:
1. Корреляция, даже статистически высокозначимая, должна характеризоваться достаточным числом наблюдений в коррелирующих переменных (не менее 20 в каждой);
2. Лучше устанавливать уровень значимости (α) с поправкой на множественность сравнений, т.е. он должен быть разумно низким, например, ≤0,01 или даже ≤0,001 – это повышает вероятность того, что такая корреляция не будет являться результатом случайного совпадения значений анализируемых признаков;
3. Каждая выявленная корреляционная зависимость должна получать четкое логическое обоснование, подтверждая некоторый известный науке феномен либо внятную, обоснованную гипотезу экспериментаторов.
Существует универсальная мера качества (объясняющей способности) причинных статистических моделей, применяющаяся, главным образом, в дисперсионном и регрессионном анализах (см. далее), но также и при вычислении коэффициентов корреляции. Это т.н. доля объясненной дисперсии, которая рассчитывается по формуле: r 2 ×100 (%). Более точно – это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели) в общей дисперсии зависимой переменной. Чем больше величина доли объясненной дисперсии, тем выше качество объясняющей модели.
Источник: studopedia.info
Корреляционный анализ
В статье рассматриваются определения корреляции,корреляционного анализа и коэффициента корреляции. Дается определение корреляционной связи и ее основных характеристик.
Ключевые слова
КОРРЕЛЯЦИОННЫЕ ПОЛЯ, КОРРЕЛЯЦИЯ, КОРРЕЛЯЦИОННЫЙ АНАЛИЗ, КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Текст научной работы
Исследователей нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых выборках. Например, такая связь может наблюдаться между погрешностью аппаратной обработки экспериментальных данных и величиной скачков сетевого напряжения. Другим примером может служить связь между пропускной способностью канала передачи данных и соотношением сигнал/шум.
В 1886 году английский естествоиспытатель Френсис Гальтон для обозначения характера подобного рода взаимодействий ввёл термин «корреляция». Позже его ученик Карл Пирсон разработал математическую формулу, позволяющую дать количественную оценку корреляционным связям признаков.
Зависимости между величинами (факторами, признаками) разделяют на два вида: функциональную и статистическую.
При функциональных зависимостях каждому значению одной переменной величины соответствует определенное значение другой переменной. Кроме того, функциональная связь двух факторов возможна только при условии, что вторая величина зависит только от первой и не зависит ни от каких других величин. В случае зависимости величины от множества факторов, функциональная связь возможна, если первая величина не зависит ни от каких других факторов, кроме входящих в указанное множество.
При статистической зависимости изменение одной из величин влечёт изменение распределения других величин, которые с определенными вероятностями принимают некоторые значения.
Значительно больший интерес представляет другой частный случай статистической зависимости, когда существует взаимосвязь значений одних случайных величин со средним значением других, при той особенности, что в каждом отдельном случае любая из взаимосвязанных величин может принимать различные значения.
Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией.
Корреляционный анализ — метод, позволяющий обнаружить зависимость между несколькими случайными величинами.
Корреляционный анализ решает две основные задачи:
- Первая задача заключается в определении формы связи, т.е. в установлении математической формы, в которой выражается данная связь. Это очень важно, так как от правильного выбора формы связи зависит конечный результат изучения взаимосвязи между признаками;
- Вторая задача состоит в измерении тесноты, т.е. меры связи между признаками с целью установить степень влияния данного фактора на результат. Она решается математически путем определения параметров корреляционного уравнения.
Затем проводятся оценка и анализ полученных результатов при помощи специальных показателей корреляционного метода (коэффициентов детерминации, линейной и множественной корреляции и т.д.), а также проверка существенности связи между изучаемыми признаками.
Методами корреляционного анализа решаются следующие задачи:
- Взаимосвязь. Есть ли взаимосвязь между параметрами?
- Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым;
- Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.
Корреляция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). Суть ее заключается в том, что при изменении значения одной переменной происходит закономерное изменение (уменьшению или увеличению) другой переменной.
Для определения наличия взаимосвязи между двумя свойствами используется коэффициент корреляции.
Коэффициент корреляции р для генеральной совокупности, как правило, неизвестен, поэтому он оценивается по экспериментальным данным, представляющим собой выборку объема n пар значений (xi, yi), полученную при совместном измерении двух признаков Х и Y. Коэффициент корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции). Его принято обозначать символом r.
К основным свойствам коэффициента корреляции относятся:
- Коэффициенты корреляции способны характеризовать только линейные связи, т.е. такие, которые выражаются уравнением линейной функции. При наличии нелинейной зависимости между варьирующими признаками следует использовать другие показатели связи;
- Значения коэффициентов корреляции — это отвлеченные числа, лежащее в пределах от -1 до +1, т.е. -1 < r < 1;
- При независимом варьировании признаков, когда связь между ними отсутствует, r = 0;
- При положительной, или прямой, связи, когда с увеличением значений одного признака возрастают значения другого, коэффициент корреляции приобретает положительный (+) знак и находится в пределах от 0 до +1, т.е. 0 < r < 1;
- При отрицательной, или обратной, связи, когда с увеличением значений одного признака соответственно уменьшаются значения другого, коэффициент корреляции сопровождается отрицательным (–) знаком и находится в пределах от 0 до –1, т.е. -1 < r
- Чем сильнее связь между признаками, тем ближе величина коэффициента корреляции к ô1ô. Если r = ± 1, то корреляционная связь переходит в функциональную, т.е. каждому значению признака Х будет соответствовать одно или несколько строго определенных значений признака Y;
- Только по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками. Этот параметр зависит от числа степеней свободы k = n –2, где: n — число коррелируемых пар показателей Х и Y. Чем больше n, тем выше достоверность связи при одном и том же значении коэффициента корреляции.
Рассчитывается коэффициент корреляции по следующей формуле:
где x — значение факторного признака; y — значение результативного признака; n — число пар данных.
Корреляция изучается на основании экспериментальных данных, представляющих собой измеренные значения xi,yi двух признаков x,y. Если экспериментальных данных сравнительно немного, то двумерное эмпирическое распределение представляется в виде двойного ряда значений xi,yi . При этом корреляционную зависимость между признаками можно описывать разными способами. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т. д.
Когда исследуется корреляция между количественными признаками, значения которых можно точно измерить в единицах метрических шкал, то очень часто принимается модель двумерной нормально распределенной генеральной совокупности. Такая модель отображает зависимость между переменными величинами x и y графически в виде геометрического места точек в системе прямоугольных координат. Эта графическая зависимость называется диаграммой рассеивания или корреляционным полем.
Данная модель двумерного нормального распределения (корреляционное поле) позволяет дать наглядную графическую интерпретацию коэффициента корреляции, т.к. распределение в совокупности зависит от пяти параметров:
- математических ожиданий E[x], E[y] величин x,y;
- стандартных отклонений px, py случайных величин x,y;
- коэффициента корреляции p, который является мерой связи между случайными величинами, х и у. Приведем примеры корреляционных полей.
Если р = 0, то значения xi,yi, полученные из двумерной нормальной совокупности, располагаются на графике в пределах области, ограниченной окружностью. В этом случае между случайными величинами x и y отсутствует корреляция, и они называются некоррелированными. Для двумерного нормального распределения некоррелированность означает одновременно и независимость случайных величин x и y.
Если р = 1 или р = -1, то говорят о полной корреляции, то есть между случайными величинами x и y существует линейная функциональная зависимость.
При р = 1 значения xi,yi определяют точки, лежащие на прямой линии, имеющей положительный наклон (с увеличением xi значения yi также увеличиваются).
При р = -1 прямая имеет отрицательный наклон.
В промежуточных случаях, когда -1< p i,yi точки попадают в область, ограниченную некоторым эллипсом, причём при p>0 имеет место положительная корреляция (с увеличением x значения y в целом имеют тенденцию к возрастанию), при p
Здесь же следует обратить внимание на то, что линия, вдоль которой группируются точки, может быть не только прямой, а иметь любую другую форму: парабола, гипербола и т. д. В этих случаях рассматривают нелинейную корреляцию.
Корреляционную зависимость между признаками можно описывать разными способами, в частности, любая форма связи может быть выражена уравнением общего вида y=f(x), где признак y — зависимая переменная, или функция от независимой переменной x, называемой аргументом.
Таким образом, визуальный анализ корреляционного поля помогает определить не только наличие статистической связи (линейной или нелинейной) между исследуемыми признаками, но и ее тесноту и форму.
По направлению корреляционная связь может быть положительной (прямой) и отрицательной (обратной).
При положительной линейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака — более низкие значения другого. При отрицательной корреляции соотношения обратные.
Знак коэффициента корреляции зависит от направления корреляционной связи: при положительной корреляции коэффициент корреляции имеет положительный знак, при отрицательной корреляции — отрицательный знак.
При изучении корреляционной связи важным направлением анализа является оценка степени тесноты связи. Понятие степени тесноты связи между двумя признаками возникает вследствие того, что в действительности на изменение результативного признака влияет множество факторов. При этом влияние одного из факторов может выражаться более заметно и четко, чем влияние других факторов. С изменением условий роль решающего фактора может перейти к другому признаку.
При статистическом изучении взаимосвязей, как правило, учитываются только основные факторы. Также с учетом степени тесноты связи оценивается необходимость более подробного изучения конкретной данной связи и значение практического ее использования.
В общем, знание количественной оценки тесноты корреляционной связи позволяет решить следующую группу вопросов:
- необходимость глубокого изучения данной связи между признаками и целесообразность ее практического применения;
- степень различий в проявлении связи в конкретных условиях (сопоставление оценки тесноты связи для различных условий);
- выявление главных и второстепенных факторов в данных конкретных условиях путём последовательного рассмотрения и сравнения признака с различными факторами.
Показатели тесноты связи должны удовлетворять ряду основных требований:
- величина показателя тесноты связи должна быть равна или близка к нулю, если связь между изучаемыми признаками (процессами, явлениями) отсутствует;
- при наличии между изучаемыми признаками функциональной связи величина показателя тесноты связи должна быть равна единице;
- при наличии между признаками корреляционной связи абсолютное значение показателя тесноты связи должно выражаться правильной дробью, которая по величине тем больше, чем теснее связь между изучаемыми признаками (стремится к единице).
Корреляционная зависимость определяется различными параметрами, среди которых наибольшее распространение получили парные показатели, характеризующие взаимосвязь двух случайных величин: коэффициент ковариации (корреляционный момент) и линейный коэффициент корреляции (коэффициент корреляции Пирсона).
Сила связи определяется абсолютным значением показателя тесноты связи и не зависит от направления связи.
В зависимости от абсолютного значения коэффициента корреляции p корреляционные связи между признаками по силе делятся следующим образом:
- сильная, или тесная (при p >0,70);
- средняя (при 0,50
- умеренная (при 0,30
- слабая (при 0,20
- очень слабая (при p <0,19).
По форме корреляционная связь может быть линейной или нелинейной.
Линейной может быть, например, связь между уровнем подготовки студента и оценками итоговой аттестации. Пример нелинейной связи — уровень мотивации и эффективность выполнения поставленной задачи. (При повышении мотивации эффективность выполнения задачи сначала возрастает, затем, при определённом уровне мотивации, достигается максимальная эффективность; но дальнейшему повышению мотивации сопутствует уже снижение эффективности.)
По направлению корреляционная связь может быть положительной (прямой) и отрицательной (обратной).
При положительной линейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака — более низкие значения другого. При отрицательной корреляции соотношения обратные.
Знак коэффициента корреляции зависит от направления корреляционной связи: при положительной корреляции коэффициент корреляции имеет положительный знак, при отрицательной корреляции — отрицательный знак.
Мониторинг команды
- Стадник А.О.
- Козин Г.А.
На сегодняшний день, существует практика применения мониторинга для улучшения команды. От команды зависит её успех и успех тех, под чьим началом она работает, её жизнеспособность в различных условиях, эффективность, экономическая целесообразность. Иными словами, мониторинг — это система, на основе результатов который принимаются меры, обеспечивающие эффективную командную работу.
Формирование доверия в группе и энергии единства в команде
- Мягков И.А.
В статье в рамках изучения лидерства и формирования команды мной рассмотрены такие понятия как «доверие в группе» и «энергия единства». В ходе анализа данных понятий я смог выделить критерии и факторы, влияющие на формирование доверия в команде, а также определил мероприятия, которые могут способствовать появлению единства внутри команды. В современной теории лидерства взаимосвязь и близость доверия и единства — это уже устоявшихся и доказанный факт.
Распределение ролей в команде
- Апина М.А.
В современных компаниях всё чаще возникают трудности из-за неправильного разделения ролей в команде. Удачно созданная или самостоятельно сформировавшаяся команда из взаимодополняющих, уважающих друг друга специалистов в процессе совместной деятельности и неформального общения достаточно быстро превращается в сплоченный коллектив с общим видением цели и единой системой ценностных ориентаций, что оказывает значительное влияние на производительность труда.
Конфликты в профессиональной среде
- Елисеева О.А.
В статье отражена значимость конфликтов в процессе трудовой деятельности, их влияние на трудовой коллектив. Рассматривается почему возникают конфликты, к чему они могут привести, где проявляются. Перечисляются причины, лежащие в основе конфликтных ситуаций.
Проблемы обновления команды
- Ахмедзаде Р.Н.
Команда в современных условиях деятельности организаций любого профиля является незаменимой составляющей. Обновление команды — это крайне ответственный процесс, требующий предельной внимательности со стороны руководителя. Команда является определяющим элементом деятельности любой компании, поскольку командная работа намного эффективнее работы отдельных сотрудников. В данной статье рассматриваются проблемы, связанные с обновлением команды.
Список литературы
- Аблеева, А. М. Формирование фонда оценочных средств в условиях ФГОС [Текст] / А. М. Аблеева, Г. А. Салимова // Актуальные проблемы преподавания социально-гуманитарных, естественно — научных и технических дисциплин в условиях модернизации высшей школы : материалы международной научно-методической конференции, 4-5 апреля 2014 г. / Башкирский ГАУ, Факультет информационных технологий и управления. — Уфа, 2014. — С. 11-14.
- Ганиева, А.М. Статистический анализ занятости и безработицы [Текст] / А.М. Ганиева, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 315-316.
- Исмагилов, Р. Р. Творческая группа — эффективная форма организации научных исследований в высшей школе [Текст] / Р. Р. Исмагилов, М. Х. Уразлин, Д. Р. Исламгулов // Научно-технический и научно-образовательный комплексы региона : проблемы и перспективы развития : материалы научно-практической конференции / Академия наук РБ, УГАТУ. — Уфа, 1999. — С. 105-106.
- Исламгулов, Д.Р. Компетентностный подход в обучении: оценка качества образования [Текст] / Д.Р. Исламгулов, Т.Н. Лубова, И.Р. Исламгулова // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 62-69.
- Исламгулов, Д. Р. Научно-исследовательская работа студентов — важнейший элемент подготовки специалистов в аграрном вузе [Текст] / Д. Р. Исламгулов // Проблемы практической подготовки студентов в вузе на современном этапе и пути их решения : сб. материалов науч.-метод. конф., 24 апреля 2007 года / Башкирский ГАУ. — Уфа, 2007. — С. 20-22.
- Лубова, Т.Н. Основа реализации федерального государственного образовательного стандарта – компетентностный подход [Текст] / Т.Н. Лубова, Д.Р. Исламгулов, И.Р. Исламгулова// БЪДЕЩИТЕ ИЗСЛЕДОВАНИЯ – 2016: Материали за XII Международна научна практична конференция, 15-22 февруари 2016. – София: Бял ГРАД-БГ ООД, 2016. – Том 4 Педагогически науки. – C. 80-85.
- Лубова, Т.Н. Новые образовательные стандарты: особенности реализации [Текст] / Т.Н. Лубова, Д.Р. Исламгулов // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 79-84.
- Лубова, Т.Н. Организация самостоятельной работы обучающихся [Текст] / Т.Н. Лубова, Д.Р. Исламгулов // Реализация образовательных программ высшего образования в рамках ФГОС ВО: материалы Всероссийской научно-методической конференции в рамках выездного совещания НМС по природообустройству и водопользованию Федерального УМО в системе ВО. / Башкирский ГАУ. — Уфа, 2016. — С. 214-219.
- Лубова, Т.Н. Основа реализации федерального государственного образовательного стандарта – компетентностный подход [Текст] / Т.Н. Лубова, Д.Р. Исламгулов, И.Р. Исламгулова // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 85-93.
- Саубанова, Л.М. Уровень демографической нагрузки [Текст] / Л.М. Саубанова, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 321-322.
- Фахруллина, А.Р. Статистический анализ инфляции в России [Текст] / А.Р. Фахруллина, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 323-324.
- Фархутдинова, А.Т. Рынок труда в Республике Башкортостан в 2012 году [Электронный ресурс] / А.Т. Фархутдинова, Т.Н. Лубова // Студенческий научный форум. Материалы V Международной студенческой электронной научной конференции: электронная научная конференция (электронный сборник). Российская академия естествознания. 2013.
Цитировать
Дашкина, Д.В. Корреляционный анализ / Д.В. Дашкина. — Текст : электронный // NovaInfo, 2017. — № 58 — С. 240-247 — URL: https://novainfo.ru/article/10577 (дата обращения: 15.09.2023).
Поделиться
Настоящий ресурс содержит материалы 16+
Источник: novainfo.ru
Корреляционный анализ
В Unisender есть все для рассылок: можно создавать и отправлять клиентам письма и SMS, настроить чат-бота и делать рассылки в Telegram и даже собрать простой лендинг для пополнения базы контактов.
Корреляционный анализ — определение степени и направления связи между двумя явлениями. Суть анализа заключается в расчете коэффициента корреляции.
Коэффициент корреляции (чаще всего под ним подразумевают ко эффициент Пирсона) — это число в диапазоне от −1 до 1.
Коэффициент не связан с конкретными единицами измерения, а значит, подходит для сравнения любых величин. Например, можно определить взаимосвязь между расходами на интернет-маркетинг в рублях и посещаемостью сайта . Или между числом продающих рассылок и продажами в штуках.
При этом коэффициент корреляции просто вычислить, и он наглядно показывает связь между двумя переменными и ее направление.
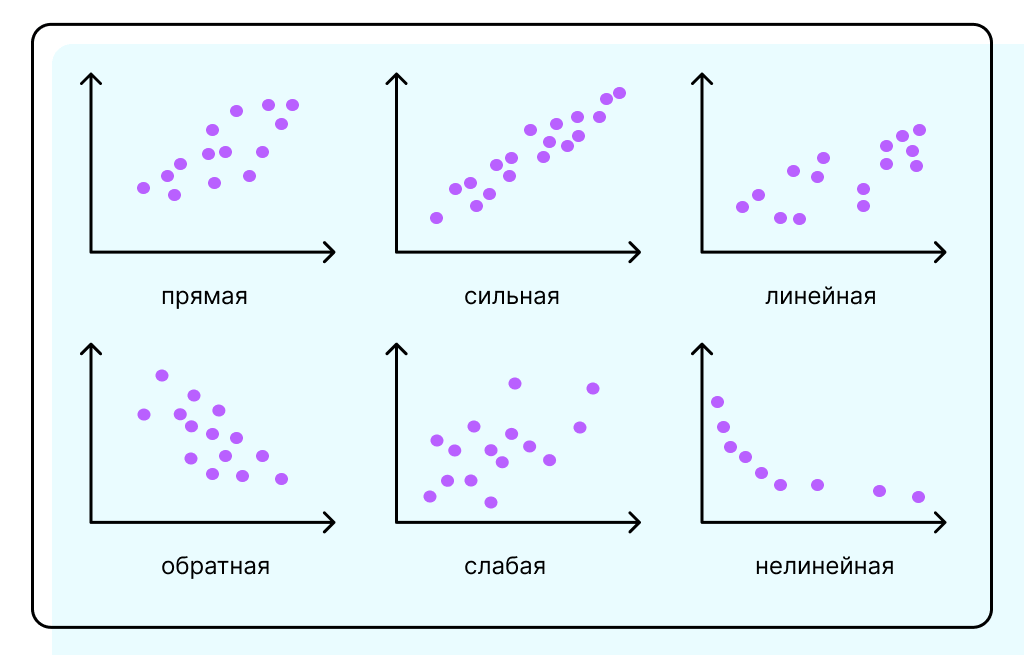
Наглядно корреляцию отображают с помощью диаграмм рассеяния. В Excel их можно построить, выбрав «Вставка-Диаграммы-Точечная»
Чем ближе коэффициент к 1, тем сильнее положительная связь между двумя переменными. Коэффициент корреляции = 1 означает, что изменению одной переменной соответствует такое же изменение другой.
Если коэффициент получается отрицательным, это означает обратную взаимосвязь: то есть при увеличении одной переменной, другая уменьшается.
Близкая к нулю корреляция показывает, что статически значимая взаимосвязь между двумя переменными отсутствует.
Зачем корреляцию используют в маркетинге
Корреляционный анализ помогает маркетологам решить большое количество самых разных задач. Если есть переменные, которые, как предполагает маркетолог, связаны друг с другом, то эту связь всегда можно проверить с помощью корреляции.
Приведем несколько примеров, когда корреляция будет полезна:
Оценить эффективность работы. Кажется, что чем больше предприниматель тратит на маркетинг, тем лучше должны быть бизнес-показатели. Но если корреляция между затратами и прибылью слабая или отрицательная, то это повод задуматься о величине и направлении вложений.
Помимо общей эффективности с помощью корреляции можно оценить, окупаются ли вложения в отдельные направления, например в SEO (корреляция затрат и конверсии на сайте) или рекламу у блогеров (затрат и продаж).
Спрогнозировать поведение потребителей. Например, чтобы рекомендовать зрителю подходящие фильмы, онлайн-кинотеатр должен понимать его вкусы. Такую информацию можно получить благодаря оценкам. Тогда можно определить корреляцию между оценками конкретного зрителя и других пользователей и показывать ему подборку картин, которые высоко оценили зрители со схожими вкусами. При этом чем больше пользователь ставит оценок, тем точнее алгоритмы предугадывают его предпочтения, а значит, тем проще удержать клиента в сервисе.
Разработать ценовую политику. Для обычных товаров работает правило: если цены падают, то продажи растут. Но есть товары Гиффена и Веблена для которых эта закономерность не действует. Корреляция с помощью прошлых данных по сбыту поможет определить, к каким группам относятся конкретные товары. Это пригодится при планировании скидок и других маркетинговых мероприятий, связанных с ценообразованием.
Как вычислить корреляцию
В Excel корреляцию можно вычислить с помощью функций КОРРЕЛ или PEARSON .
Обратите внимание, что аномальные показатели в данных (выбросы или пропуски) могут исказить значение коэффициента корреляции. Поэтому не забудьте провести их предварительную очистку.
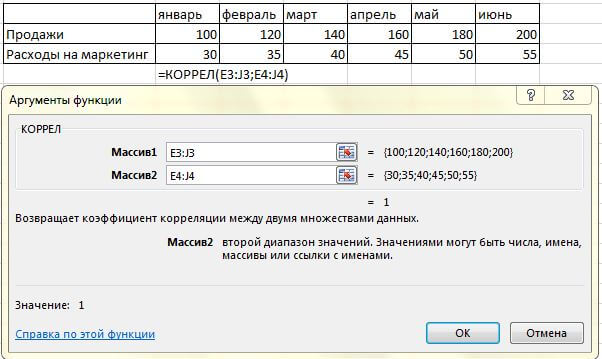
Пример вычисления корреляции между объемом продаж и расходами на маркетинг
Анализ корреляции часто дополняют исследованием регрессии — проводят корреляционно-регрессионный анализ.
Регрессия позволяет предсказать значение одной переменной (зависимой) под влиянием изменения другой (независимой) или нескольких других переменных. При этом исследователь сам определяет, какую переменную считать зависимой, а какую нет.
Например, если маркетолог обнаружил сильную положительную корреляцию между затратами на рекламу (независимая переменная) и продажами (зависимая переменная), то он может построить уравнение регрессии для прогнозирования того, насколько вырастет сбыт, если расходы на рекламу увеличатся на единицу.
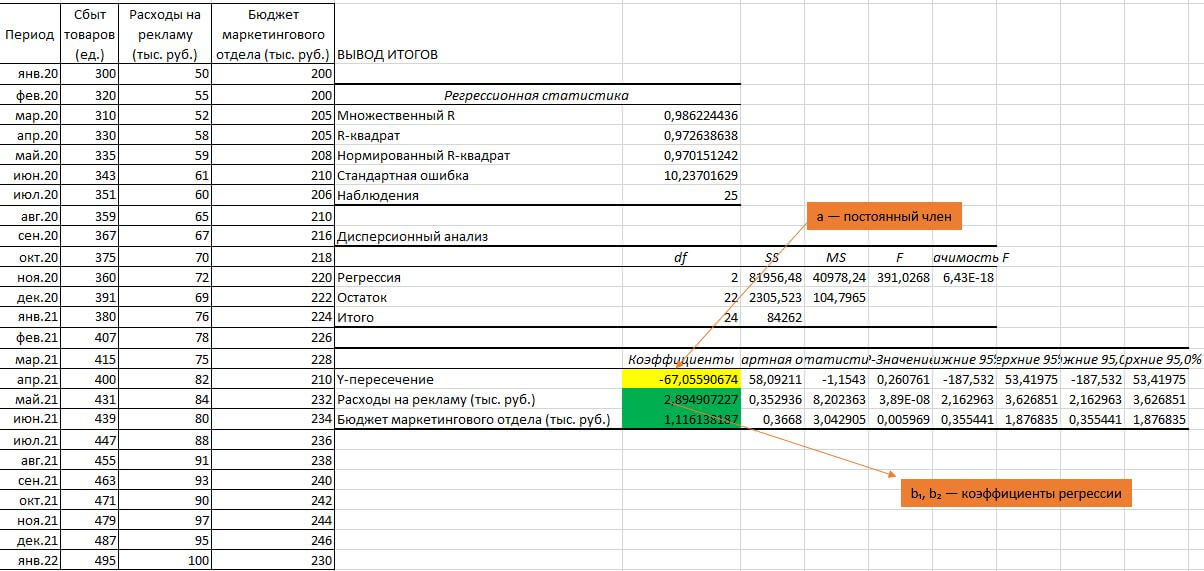
В Excel корреляционно-регрессионный анализ можно провести с помощью инструмента «Регрессия» из Пакета Анализ данных.
На скриншоте ниже показан пример анализа связи между зависимой переменной (сбытом) и независимыми переменными (рекламным и маркетинговым бюджетом). Уравнение регрессии выглядит следующим образом: Y = -67 + 2,89* (расходы на рекламу) + 1,12*(бюджет маркетингового отдела). Подставляя соответствующие числа, можно получить значение продаж за конкретный месяц
Если нужно вычислить степень взаимосвязи между несколькими параметрами , используют корреляционную матрицу (correlation matrix). Это таблица, которая содержит коэффициенты корреляции для каждой пары переменных.
Чтобы построить корреляционную матрицу в Excel, используют инструмент Корреляция из пакета Анализ данных.
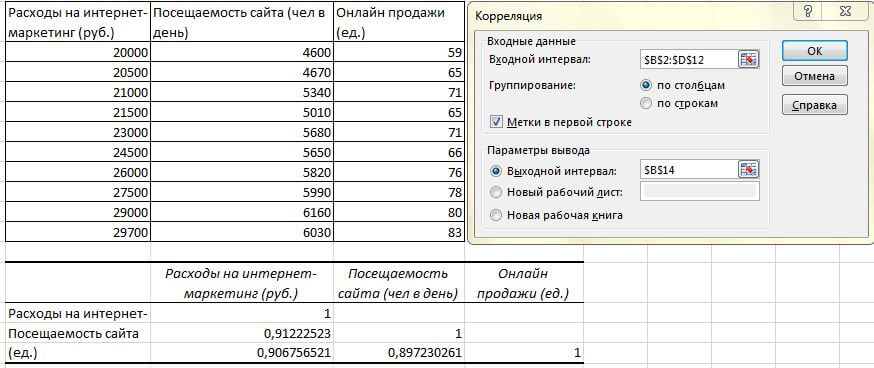
Пример построения корреляционной матрицы в Excel. Определяем взаимосвязь между посещаемостью сайта, расходами на маркетинг и продажами
Для определения корреляции можно использовать не только коэффициент корреляции Пирсона, но и ранговый коэффициент корреляции Спирмена . Этот показатель определяет силу и направление связи между двумя группами предварительно ранжированных переменных.
Ранговый коэффициент удобно использовать, когда:
- данные лучше смотрятся в ранговой форме (балльные оценки некоторых критериев, рейтинги или группировка близких числовых значений),
- изменение одной переменной связано с изменением другой переменной, но эта связь не носит линейный характер.
Алгоритм вычисления коэффициента Спирмена в Excel:
- упорядочить две группы чисел;
- использовать функцию РАНГ.СР для ранжирования;
- использовать функцию КОРРЕЛ — как значения в ней берутся ранги.
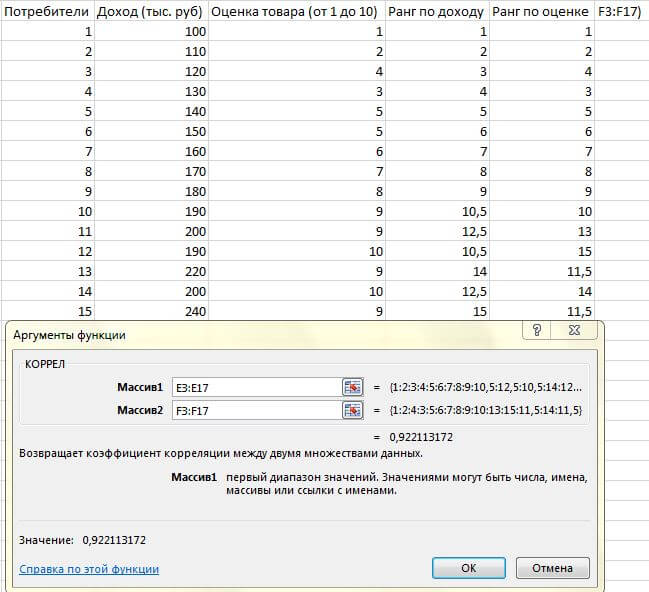
Ниже приведен пример вычисления рангового коэффициента корреляции Спирмена в Excel
Особенности корреляции, которые важно учитывать при анализе
Не показывает причинно-следственной связи между двумя переменными . Важнейшая черта корреляции. Даже если коэффициент корреляции = 1 (-1), это не значит, что изменение одной переменной приведет к изменению другой.
Есть две переменные: расходы на маркетинг и продажи. Маркетолог вычисляет корреляцию и находит, что она близка к 1. Но ведь продажи могут расти, к примеру, под влиянием сезонного тренда или рекламных акций, а расходы на маркетинг просто удачно вписались в общую картину.
Противоположная ситуация: расходы на маркетинг растут, но идёт спад продаж.
Налицо отрицательная корреляция. Но это снова может быть совпадением во времени.
В обеих ситуациях требуется более тщательный анализ: рассмотрение других переменных, учёт сезонности, проверка данных за другие периоды времени.
Может меняться со временем . Например, взяли данные за лето, и они показали слабую корреляцию. Но анализ тех же переменных в зимний период может показать корреляцию, близкую к 1.
Не показывает, какая переменная влияет на другую . Например, расходы на маркетинг могут влиять на показатели продаж. Но ведь и выросшие продажи также могут привести к тому, что топ-менеджеры решат увеличить расходы на маркетинг.
Не показывает зависимость, если она нелинейная . Например, увеличение расходов на маркетинг первоначально приводит к росту продаж. Однако, начиная с какого-то момента, дополнительные расходы больше не стимулируют сбыт, а наоборот, приводят к его снижению (в экономической теории — закон убывающей отдачи).
Приведенные примеры показывают, что вычислить один только коэффициент корреляции мало, нужно более подробно анализировать имеющиеся данные.
Источник: www.unisender.com
