Разберем еще один, более широко используемый метод решения игровых задач, который называется методом выигрышных позиций. С его помощью можно решить многие задачи, которые решаются как с помощью симметрии, так и дополнения до фиксированного числа.
Суть метода: делим всю доску (или все возможные ходы) на два вида полей — выигрывающие и проигрывающие (причем под это определение попадают все рассматриваемые клетки или ходы). После этого стратегия играющего заключается в том, чтобы делать свой ход на выигрывающие клетки (или делать выигрывающие ходы). Данный метод пригоден почти для всех игровых задач.
Рассмотрим применение данного метода на конкретной задаче.
10). Ладья стоит на поле al. За ход можно сдвинуть ее на любое число клеток вправо или вверх. Выигрывает тот, кто поставит ее на поле h8. Кто выиграет при правильной игре?
Решение. Разобьем шахматную доску на выигрышные и проигрышные поля (расстановка выигрышных и проигрышных полей на доске определяется только для одного из игроков).
Выигрышная стратегия в теории игр | 8/50 урок Информатики | Задания 19-21 ЕГЭ
Что значит позиция выигрышная или проигрышная?
Позиция будет выигрышной для игрока-победителя, если:
а) Завершающая позиция игры для него выигрышная, т. е. он делает последний ход.
б) Из любой выигрышной позиции за один ход нельзя попасть в выигрышную.
в) Из любой проигрышной позиции за один ход можно попасть в выигрышную.
Начинаем с начальной позиции. Ладья стоит на поле al. Поле h8 выигрышное. Пометим его знаком «+». Значит все остальные поля последней строки и последнего столбца доски проигрышные, т. е. поставим на них знак «-».
Несложно понять, что поле g7 также выигрышное (с него все ходы ведут в проигрышные поля). Следовательно, все остальные поля седьмой горизонтали и седьмого столбца проигрышные и т. д. Расставляя «+» на выигрышные поля, и «-» на проигрышные, мы замечаем, что если ладья стоит на главной диагонали, тогда клетка выигрышная, если же она там не стоит, тогда проигрышная. И тот, кто поставил ладью на поле со знаком «+», выигрывает, а тот, кто поставил ладью на поле со знаком «-», — проигрывает.
Таким образом выигрывает второй игрок, так как первому игроку первым ходом нужно идти на поле со знаком «-»
Рассмотрим еще одну задачу, где действует данный метод, но где разбиение на выигрышные и проигрышные позиции уже не столь просто, как в предыдущей задаче.
11). Имеются две кучки конфет: в одной — 20, в другой — 21. За ход нужно съесть все конфеты в одной из кучек, а вторую разделить на две необязательно равные кучки. Проигрывает тот, кто не может сделать ход. Кто выиграет?
Решение. Если мы решили использовать метод выигрышных позиций, то нам нужно найти эти выигрышные позиции. Чтобы их найти, рассмотрим простейшие случаи.
Простейшая выигрышная позиция для того игрока, кто ее создал (т. е. «сходил» последним): это 1 и 1. Понятно, что в этом случае побеждает тот, кто ходит вторым, так как у первого игрока нет хода.
Очевидно, что позиция 2 и 1 выигрышная для первого и проигрышная для второго.
ЕГЭ по информатике. Теория игр. Поиск выигрышной стратегии. Задания №19, 20, 21
Если 3 и 1, тогда второй вновь с победой, как несложно убедиться простой проверкой, так как есть ровно два хода.
Когда в кучках 3 и 2, победа у первого (убираем 3, делим 2).
Если же 3 и 3, тогда победа вновь возвращается ко второму, что можно показать простым перебором и т. д.
Замечаем закономерность: если в каждой из кучек по нечетному числу конфет, тогда позиция выигрышная для второго.
Если же хотя бы в одной из кучек четное число конфет, то такая позиция выигрышная для первого.
Несложно понять, что когда в обеих кучках по нечетному числу конфет, то за один ход нельзя получить такую же позицию, так как при разделении любого нечетного числа на два слагаемых одно из них будет четным. Однако если хотя бы в одной из кучек четное (ненулевое) число конфет, то ее несложно разбить на два нечетных слагаемых. Таким образом мы можем разбить все позиции на выигрышные и проигрышные с учетом того, сколько конфет в кучках. И задача выигрывающего делать ход на выигрышные позиции.
После этого уже понятно, кто выиграет в данной по условию игре и как ему этого добиться.
Делим все возможные ходы на «выигрышные» и «проигрышные». Если после разбиения получились две кучки с нечетным числом конфет, тогда назовем такую позицию «выигрышной», а все остальные — «проигрышные».
Стратегия победителя заключается в том, что он делает ход на «выигрышные» поля. Так как первый может сделать ход на «выигрышное» поле, а хода с одного «выигрышного» поля на другое нет, и с любого «проигрышного» поля за один ход можно попасть на «выигрышное», то побеждает начинающий. Своим первым ходом он может съест кучку из 21 конфеты, а кучу с 20 конфетами разделить на две, в которых нечетное количество конфет в обеих кучках (например, 19 и 1). Заметим, что последняя позиция, когда две кучки, по одной конфете в каждой, выигрышная, т. е. последний ход сделает первый.
Решим еще одну задачу методом выигрышных и проигрышных позиций.
12). На концах клетчатой полоски 1 х 20 стоит по шашке. За ход разрешается сдвинуть любую шашку в направлении другой на одну или две клетки. Перепрыгивать через шашку нельзя. Проигрывает тот, кто не может сделать ход.
Кто выиграет при правильной игре?
Решение. Сначала перенумеруем поля доски. Несложно понять, что одну из шашек можно считать неподвижной, так как в любой случае за один ход, сделанный обоими игроками, расстояние между шашками сокращается не менее, чем на 2 клетки (а именно это и является главным в задаче). Поэтому можно считать, что оба из игроков передвигают только одну из шашек. Расставляя знаки «+» и «-» на клетках доски согласно метода решения задачи с конечной позиции, получим следующий рисунок (если первоначально шашки не занимали клеток доски, т. е. между ними было 20 полей):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Таким образом, становится понятным «выигрышная» стратегия игры первого игрока, чтобы выиграть: он должен делать ходы на клетки со знаком «+», так как с любого поля со знаком «+» нельзя за один ход попасть на поле со знаком «+», а с любого поля со знаком «—» можно, т. е. сделано разбиение всего поля на «выигрышные» и «проигрышные» поля.
Рассмотрим следующую задачу.
13). Ферзь стоит на поле cl. За ход его можно сдвинуть на любое число полей вправо или на любое число полей вверх или по диагонали вправо-вверх. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?
Решение. Решаем задачу методом выигрышных позиций. Отметим на доске выигрышные и проигрышные поля, начиная с конечной позиции.
Понятно, что h8 — «+». Все поля, с которых можно попасть на h8 за один ход, обозначаем «-». Отсюда поля g6 и f7 со знаком «+». И так далее. Таким образом мы разбили всю доску на выигрышные и проигрышные поля.
После заполнения таблицы мы видим, что выигрывает первый. Он своим первым ходом может занять поле со знаком «+», например, с5, и далее ходит на клетки со знаком «+».
Отметим, что выигрышных полей у первого игрока для первого хода несколько, а не обязательно одно.
Вот в этом и состоит один из более универсальных методов решения игровых задач: метод выигрышных позиций, т. е. разбиения игрового поля на выигрышные и проигрышные позиции.
Перечислим основные идеи, которые используются при решении задач данным методом:
· начинать поиск решения лучше с клетчатых досок, на которых малое число полей, или с небольшого количества камней, конфет или других предметов, о которых идет речь в задаче;
· разбиение доски на выигрышные и проигрышные поля лучше всего начинать с конечных позиций.
Игры – шутки
Игры – шутки – это такие игры, где для построения выигрышного алгоритма можно ничего и не знать, так как в них результат будет зависеть не от игры партнеров, а от начальных условий. Однако для этого в решении нужно заметить, что это игра-шутка, а не какая-то другая, в которой нужно искать выигрышную стратегию.
Отметим, что часто для нахождения идеи решения задачи можно использовать «метод маленьких чисел», т. е. начинать поиск решения с небольших чисел, который мы уже упоминали в предыдущих разделах.
14). Двое по очереди ломают шоколадку 6 х 8. За ход можно сделать прямолинейный разлом любого из кусков вдоль углубления. Проигрывает тот, кто не может сделать ход. Кто выиграет?
Решение. Сначала рассмотрим маленькую шоколадку, например, 1×2. Понятно, что здесь выиграет первый, так как всего один ход. А если 1×3? Тогда понятно, что второй, ходов в любом случае, всего два. А если 2×2?
Тогда, вновь понятно, что первый, потому что в игре ровно 3 хода. А если шоколадка имеет размеры 1×5? Тогда, после небольшого перебора, замечаем, что выигрывает всегда второй и ходов ровно четыре.
В чем шутка этой задачи? Да в том, что за один ход число кусочков увеличивается ровно на 1, причем совершенно не важно каким образом происходит разлом.
Поэтому при данных условиях (когда шоколадка имеет размеры 6×8) выиграет тот, кто делает «нечетные» разломы, т. е. после хода которого остается четное число кусочков шоколада. Отсюда получаем, что выиграет первый игрок, так как всего будет 48 кусочков шоколадки.
После проведенного анализа для нахождения решения также понятно, кто выиграет, когда шоколадка будет других размеров, например, 7×9. Ясно, что тогда побеждает второй, так как после его хода всегда остается нечетное число кусочков и в игре будет сделано ровно 62 хода.
Отсюда можно сделать общий вывод:
Если число кусочков шоколадки четно, тогда побеждает первый, если число нечетно, тогда второй.
Рассмотрим еще некоторые задачи.
15). Имеется три кучки камней: в первой — 10, во второй — 15, в третьей — 20. За ход можно разбить любую кучку на две меньшие. Проигрывает тот, кто не может сделать ход. Кто выиграет?
Решение. И это задача-шутка. Количество возможных ходов для раскладывания кучек: 45 – 3 = 42. Поэтому, как бы ни ходил первый игрок, при его ходе всегда будет четное число кучек. При ходе же второго игрока количество кучек будет всегда нечетно.
Значит, победит первый игрок, так как по окончании игры всегда остается ровно 45 кучек по одному камню в каждой.
16). Малыш и Карлсон делят конфеты. Их всего 101 штука. Если после их дележа количества конфет у каждого из них будут двумя взаимно простыми числами, тогда выиграет Малыш, если же нет, тогда Карлсон. Кто выиграет?
Решение. Это задача-шутка. Здесь всегда выигрывает Малыш, ибо если сумма двух чисел равна 101, то они не могут быть не взаимно простыми (иначе их сумма — 101 — также имела бы среди делителей их общий делитель, а 101 — простое число).
Исследования решений некоторых задач в общем виде
А сейчас вернемся к некоторым уже решенным задачам и исследуем решения в общем виде.
Задача № 2. Двое по очереди ставят слонов в клетки шахматной доски 8×8 так, чтобы слоны не били друг друга. Проигрывает тот, кто не может сделать ход. Кто выиграет?
При решении данной задачи использовалась осевая симметрия: ставя своего слона симметрично слону относительно оси симметрии шахматной доски 8×8, поставленному первым игроком, выигрывает второй игрок.
Исследуем решение данной задачи при различных размерах доски. Если бы доска была размером 7×7 (или 9 х 9), тогда идею осевой симметрии уже нельзя использовать, ибо первый может поставить своего слона в центр и у второго нет хода на это. Необходимо использовать в данном случае центральную симметрию: первый игрок ставит первым своим ходом слона в центр доски, а потом на любой ход противника отвечает симметричным относительно центра ходом. И тогда для первого игрока всегда найдется возможность сделать последний ход.
Итак, в задаче со слонами на шахматной доске возможны следующие случаи:
· если квадратная доска имеет четные размеры 2k х 2k, то при решении задачи используем симметрию относительно оси, которая проходит параллельно одной из сторон доски. Второй игрок делает ходы, симметричные ходам противника относительно данной оси и у него всегда найдется возможность сделать ход независимо от хода противника. Выигрывает второй игрок.
· если квадратная доска имеет нечетные размеры (2k + 1) х (2k + 1), то при решении задачи используем центральную симметрию: после того, как первый ставит своим первым ходом слона в центр доски, то он выиграет, действуя центрально симметрично ходам второго игрока. У него уже есть такая возможность!
Задача № 5. На окружности расставлено 20 точек. За ход можно соединить любые две отрезком, не пересекающим отрезки, проведенные ранее. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?
При решении этой задачи мы располагали точки в вершине правильного 20-угольника и дальше использовали симметрию относительно диаметра.
Ну а если точки расположены не в вершинах правильного 20-угольника, а произвольно? Тогда ходы будут теми же самыми, только симметрия будет подразумеваться по номерам вершин. Если первый ходит вначале, соединяя 10-ю и 20-ю точки, второй — i — ю и j-ю, то первый отвечает соединением (20 — i)-й и (20 — j)- йточек. И так далее на каждом последующем шаге.
Ну а если точек не 20, а 2k + 1 (нечетное количество)? Тогда необходимо первому игроку первым ходом провести хорду, соединяющую 1-ю и k + 1 — ю точки, в следствии чего окружность разобьется на две части: в одной – (k – 1) точка, а в другой — k точек. Из этих двух количеств точек одно отличается от другого на единицу. Поэтому при любом ходе второго игрока, для первого игрока найдется ход, симметричный относительно проведенной хорды. И последняя точка, из которой нельзя сделать ход, «достанется» второму игроку.
Задача № 6. Двое играют в игру. Ходы, которые делаются по очереди, заключаются в том, что из кучки в 50 камней убирается любое число камней от 1 до 5. Выигрывает тот, кто возьмет последний камень. Кто выиграет в данной игре?
Решение данной задачи основано на дополнении хода противника до числа 6. Выигрывает в данной игре первый, беря из кучки два камня и оставляя 48 камней. Далее после его последующих ходов в кучке будет оставаться соответственно 42, 36, 30, 24, 18, 12, 6, 0, таким образом последний камень забирает первый игрок.
Теперь рассмотрим задачу в общем виде и найдем «правило», позволяющее выбрать правильную стратегию при решении задачи..
Пусть лежат k камней. Играют двое, ходят по очереди. За один ход можно брать любое число камней от 1 до t. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?
Найдем остаток от деления k на t + 1. Обозначим его a.
· Пусть a ≠ 0. Первый игрок первым ходом должен взять a камней. Второй игрок будет брать за один ход любое количество камней от 1 до t, тогда первый игрок своими ходами должен дополнять ходы противника до t + 1. И тогда последний камень обязательно заберет первый игрок, а значит выиграет. Действительно, если от k отнять a, то получим число, которое нацело делится на t + 1. За один ход второй и первый игроки берут вместе t + 1 камень, причем последним берет первый игрок. Так как k – a нацело делится на t + 1, то первый игрок выиграет.
· Пусть a = 0, тогда по сравнению с предыдущим случаем игроки как бы поменялись местами (число уже сразу нацело делится на t + 1), а поэтому выигрывает второй игрок.
Задача № 10. Ладья стоит на поле al. За ход можно сдвинуть ее на любое число клеток вправо или вверх. Выигрывает тот, кто поставит ее на поле h8. Кто выиграет при правильной игре?
При решении данной задачи была составлена следующая схема выигрышных и проигрышных позиций, из которой следовало, что при правильной игре выигрывать будет всегда второй игрок.
Изменим ситуацию в задаче и рассмотрим данную задачу для доски m х n. Исследуем решение данной задачи в общем виде.
Правое верхнее поле выигрышное. Пометим его знаком «+».Значит все остальные поля последней строки и последнего столбца доски проигрышные, т. е. поставим на них знак «-». Рассуждая аналогично предыдущей задаче, расставим выигрышные позиции (знаки «+») в диагонали клеток, ведущих с правой верхней клетки. Тогда все остальные поля отмеченных горизонталей и отмеченных столбцов проигрышные (m горизонталей и m столбцов).
Теперь очевидно, что при правильной игре выигрывать будет первый игрок: первым ходом он должен пойти на n – m (n > m) полей вправо (или m – n полей вверх в случае m > n), попав на поле выигрышной позиции. Далее второй игрок своим ходом будет попадать только на проигрышные позиции, с которых первый игрок должен возвращаться на диагональ выигрышных позиций.
1) Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. Киров: АСА, 1994.
2) Гусев В.А., Орлов И.А., Розенталь А.Л. Внеклассная работа по математике в 6-8 классах. М.: Просвещение, 1984.
3) Петров Н.Н. Математические игры. Ижевск: УдГУ, (1 изд.) 1994.
4) Яглом И.М. Две игры со спичками // Квант. 1971. №2.
5) Л. М. Лихтарников. Задачи мудрецов. М.: Просвещение, 1996.
6) Т. П. Бахтина. Готовимся к олимпиадам, турнирам и математическим боям. Минск: АВЕРСЭВЬ, 2004.
7) А. В. Спивак. Тысяча и одна задачи по математике. М.: Просвещение, 2002.
Источник: poisk-ru.ru
Презентация на тему Задачи с выигрышной стратегией
Игровые задачи В игровых задачах необходимо грамотно сформулировать стратегию игры и доказать, что она действительно ведёт к выигрышу. Обычный вопрос в таких задачах: «Кто и как выиграет при правильной игре?»
- Главная
- Разное
- Задачи с выигрышной стратегией
Слайды и текст этой презентации
Слайд 1Задачи с выигрышной стратегией (игровые задачи)
Учитель математики
МОУ «Будогощская СОШ»
Кондратьева Наталья Владимировна

Слайд 2Игровые задачи
В игровых задачах необходимо грамотно сформулировать стратегию
игры и доказать, что она действительно ведёт к выигрышу. Обычный
вопрос в таких задачах: «Кто и как выиграет при правильной игре?»

Слайд 3Некоторые типы игровых задач:
Игры-шутки;
Игры с симметрией;
Игры, в которых стратегия дополнение
до фиксированного числа.

Слайд 4Игры-шутки
Задачи – шутки – это такие игры, где
для построения выигрышного алгоритма можно ничего и не знать, так
как в них результат будет зависеть не от игры партнеров, а от начальных условий. Однако для этого в решении нужно заметить, что это задача-шутка, а не какая-то другая, в которой нужно искать выигрышную стратегию. На самом деле, нет никакой стратегии (а нас хотят обмануть, что она якобы есть!) Просто. как бы кто ни ходил, либо всегда выиграет первый игрок (тот, кто начинает игру), либо всегда второй.

Слайд 51. Задачи-шутки
Задача 1.
Двое по очереди ломают шоколадку 3×4.
За ход можно разломать любой кусок по прямой линии
между дольками. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

Слайд 6Решение:
Долек всегда будет 3×4=12 штук, а
шоколадка в начале была одна. Заметим, что на каждом ходу
один кусок шоколадки всегда разламывается на 2, т.е. количество различных кусков шоколадки увеличивается на 1. В начале это кол-во было равно 1, а в конце, как мы заметили, 12. Значит, игра продолжалась ровно 11 ходов. Поэтому последний (11-й) ход был обязательно ходом первого (его ходы — первый, третий и все с нечетными номерами) — и первый выиграл. Вот такая получилась шутка — как ни ходи, первый всегда выигрывает.

Слайд 7Задача 2.
Двое по очереди ломают шоколадку 5×7.
За ход можно разломать любой кусок по прямой линии между
дольками. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

Слайд 8Решить ту же задачу в общем виде, про шоколадку mxn.
Если число кусочков шоколадки четно, тогда
побеждает первый, если число нечетно, тогда второй.

Слайд 9Задача 3.
Имеется три кучки ракушек: в
первой — 5, во второй — 6, в третьей —
8. За ход можно разбить любую кучку на две меньшие. Проигрывает тот, кто не может сделать ход. Кто выиграет?
Решение

Слайд 10Решение:
И это задача-шутка. Количество возможных ходов
для раскладывания кучек: 25-3=22. Выиграет второй игрок, так как необходимо
сделать чётное количество ходов.

Слайд 11Игры с симметрией
Очень простой, но мощный и
красивый метод решения игровых задач — симметричная стратегия. Суть его
— делать каждый раз ход, симметричный ходу противника. Доказательство правильности нашей стратегии будет пользоваться тем, что после каждого нашего хода позиция симметрична: раз так, то если противник сумел сделать свой ход, то и мы сможем сделать ход, симметричный ему.

Слайд 12Задача 4.
На столе лежат две кучки
конфет, по 9 в каждой кучке. Два игрока по очереди
берут со стола любое количество конфет из какой-либо одной кучки. Выигравшим считается тот, кто берёт со стола последние конфеты. Кто и как выиграет при правильной игре?
Решение

Слайд 13 Выиграет второй игрок, который, делая ход,
берёт то же количество конфет, что и начинающий игру, но
из другой кучки, т. е. проводит симметричный ход.

Слайд 14Задача 5.
На столе лежат две кучки
спичек: в одной – 50, в другой 30 спичек. Два
игрока по очереди берут со стола любое количество спичек из какой-либо одной кучки. Выигравшим считается тот, кто берёт со стола последние спички. Кто и как выиграет при правильной игре?
Решение

Слайд 15 Выиграет начинающий игру. Первым ходом
ему следует взять 20 спичек из первой кучки, а дальше
отвечать на ход второго игрока симметричным ходом.

Слайд 16Какова стратегия?
Несложно понять общую стратегию выигрывающего, когда
в кучках произвольное число камней:
если число предметов в кучках
равное, то необходимо уравнивать число предметов в кучках после хода начинающего, выполняя симметричные (такие же) ходы. Выигрывает второй игрок.
если же число предметов в кучках неравное, тогда начинающий своим ходом уравнивает число предметов в кучках и далее действует так же как, как и в первом случае. Здесь побеждает игрок, делающий первый ход.

Слайд 17Игры, в которых стратегия — дополнение до фиксированного числа
Другая идея выигрышной стратегии в играх — дополнение
хода соперника до некоторого фиксированного числа, уменьшая каждым «совместным» ходом (т. е. ход первого и второго игрока) общее число элементов на некоторое постоянное число, что сводит игру к игре с меньшим числом элементов, т. е. более простой. Понятно, что победа в данной стратегии зависит от общего количества данных по условию элементов.

Слайд 18Задача 6.
В ромашке 8 лепестков. Два
игрока по очереди отрывают лепестки. Можно отрывать 1 или 2,
проигрывает тот,
кто не может сделать ход. Как вы думаете: кто выигрывает при «правильной игре» тот, кто начинает или тот, кто ходит вторым?

Слайд 19 Выигрывает первый игрок!
Он
отрывает 2 лепесточка..
И после каждого хода соперника
дополняет общее количество, оторванных лепестков до трёх ( т.е. 8-2=6; 6 делится на 3)

Слайд 20Задача 7.
В ромашке 10 лепестков. Два
игрока по очереди отрывают лепестки. Можно отрывать 1 или 2,
проигрывает тот,
кто не может сделать ход. Как вы думаете: кто выигрывает при «правильной игре» тот, кто начинает или тот, кто ходит вторым?

Слайд 21 Выигрывает первый игрок!
Он отрывает
1 лепесток..
И после каждого хода соперника дополняет
общее количество, оторванных лепестков до трёх ( т.е. 10-1=9; 9 делится на 3)

Слайд 22Задача 8.
В ромашке 14 лепестков. Два игрока
по очереди отрывают лепестки. Можно отрывать 1 или 2, но
только соседние лепестки. Проигрывает тот, кто не может сделать ход. Как вы думаете: кто выигрывает
при «правильной игре» тот, кто начинает или тот, кто ходит вторым?
Решение

Слайд 23 Выигрывает первый игрок!
Он отрывает 2 лепесточка..
И после каждого хода соперника дополняет общее количество, оторванных лепестков
до трёх ( т.е. 14-2=12; 12 делится на 3)

Слайд 24Задача 9.
Ладья стоит на поле a1.
Играют двое. За ход разрешается сдвинуть ладью на любое число
клеток вправо или на любое число клеток вверх. Выигрывает тот, кто поставит ладью на поле h8. Кто из игроков обладает выигрышной стратегией?
Источник: theslide.ru
Как выигрывать в шахматы – 10 ключевых моментов, которые стоит знать


Когда Вы играете на уровне 1800 и ниже, выигрыши (впрочем, как и проигрыши) достигаются довольно легко. Ведь исход многих поединков между игроками с таким рейтингом решается ошибками и зевками. И если вы сейчас находитесь именно на этой ступени развития, то наверняка мечтаете сделать свои победы стабильными.
Откроем Вам небольшой секрет – чтобы выйти на следующую шахматную орбиту, не нужно обладать фотографической памятью или просчитывать на 10 ходов вперед. Всё проще. Просто попробуйте следовать десяти рекомендациям из списка ниже.
1. Научитесь быстро развивать фигуры
Все говорят, что дебюты желательно знать досконально, и чтобы чаще побеждать, следует быть теоретически подкованным игроком. Да, у вас должно быть общее представление, как развивать фигуры и как действовать сразу после. Но главная цель любого дебюта – развить фигуры на нужные поля быстрее, чем ваш соперник. И если вы смогли это сделать, значит вы на шаг приблизились к победе в игре.
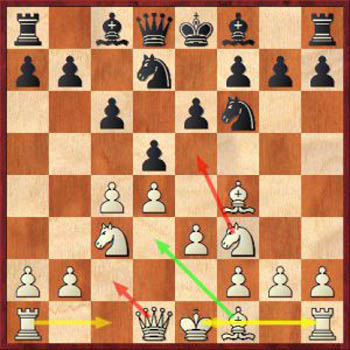
Выигрышная стратегия в шахматах №1: быстро развивайте фигуры
2. Ранняя рокировка
Ещё один очень важный ключ к победе — ранняя рокировка. Рокировка не только защищает вашего короля и уводит его подальше от центра доски. Она также активирует ладьи, подготавливает их к вступлению в игру, чтобы взять под контроль последнюю горизонталь и открытые линии. Это единственный ход, который позволяет улучшить сразу две ваши фигуры! Научитесь рокироваться в начале игры, и это поможет вам избегать многих проблем.
Некоторые игроки-любители совершают ошибку, когда отказываются от рокировки, польстившись на пешки соперника или переключившись на развитие других фигур. Это часто приводит к агрессивной атаке на их короля, и потом они платят огромную цену за восстановление.

Выигрышная стратегия в шахматах №2: Ранняя рокировка
3. Контроль центра
Контроль центра — безусловно, одна из самых значимых шахматных стратегий. Но некоторые новички не понимают, что такого важного в контроле этих четырех центральных полей: e4, d4, e5 и d5. А ведь и на самом деле — тот, кто контролирует эти поля, фактически управляет игрой. Управление центром тесно связано с одной из ключевых шахматных концепций – пространства.
Если у вас больше места, то и больше возможностей перемещать фигуры для атаки и защиты. А ваш оппонент лишен этой привилегии и находится в невыгодном положении.
Контроль над центром даёт вам нечто большее, чем просто возможность перемещать фигуры по своему усмотрению. Гораздо важнее, что это обеспечивает легкую транспортировку ваших фигур к обеим сторонам доски. Таким образом, вы получаете отличные возможности для мощной атаки, которая, в свою очередь, может привести к победе в игре.
И если вы колеблетесь и не знаете, как играть конкретную партию, вспомните, что контроль над центром обычно является выигрышной стратегией.

Выигрышная стратегия в шахматах №3: Контроль центра
4. Планируйте больше, чем на один ход вперед
Для победы в шахматах порой достаточно продумать на один ход вперед — если это лучший ход. Но, к сожалению, большинство шахматистов обычно не знают, какой ход является лучшим. Поэтому мы вынуждены анализировать глубоко несколько ходов, чтобы убедиться, что учитываем все разумные возможности.
Конечно, Вам не нужно просчитывать на 10 ходов вперед (хотя, если вы можете, то это здорово).
Вы должны попробовать рассчитать хотя бы 3 хода в глубину во всех позициях. Этой глубины будет достаточно, чтобы избежать большинства тактических ударов, с которыми сталкиваются игроки меньше 2000 ЭЛО. И если вы всегда будете рассчитывать на 3 хода вперед, то можете не сомневаться — вы выиграете немало шахматных партий!
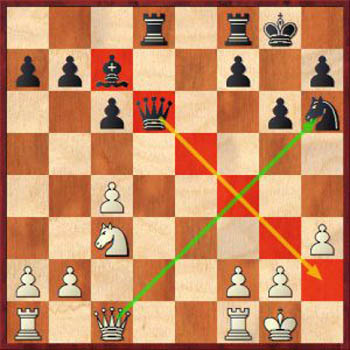
Выигрышная стратегия в шахматах №4: Думайте больше, чем на один ход вперед
5. Научитесь делать связку, вилку и сквозную атаку против фигур соперника
Связка, вилка и сквозная атака принесли за всю историю шахмат больше побед, чем все другие комбинации вместе взятые. Вот почему важно идентифицировать их и быстро находить даже в сложных позициях. Краткое напоминание о роли этой «могучей тройки»:
Связка — ситуация, когда атакующая фигура угрожает захватить другую фигуру, которая не сможет двигаться, не обнажив более ценную фигуру. Это мощный тактический элемент, поскольку он временно парализует фигуру противника, не позволяя ей полноценно участвовать в игре.
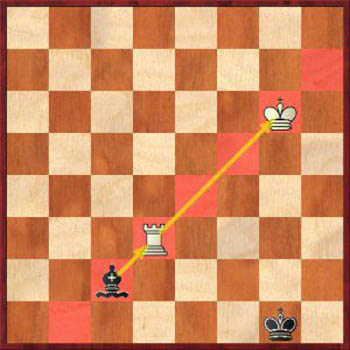
Выигрышная стратегия в шахматах №5: Связать фигуру соперника
Вилка — когда одной фигурой одновременно атакуется несколько фигур противника. Это сильный приём, т.к. он часто приводит к потере материала соперником – особенно, если есть шах королю.
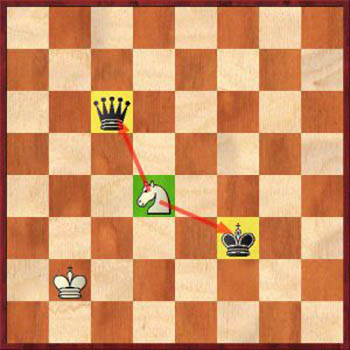
Выигрышная стратегия в шахматах №6: Вилка на фигуры соперника
Сквозная атака очень похожа на связку, но здесь сначала атакуется более ценная фигура. Когда она отходит, то теряется менее ценная фигура.
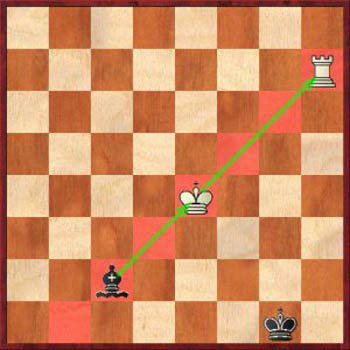
Выигрышная стратегия в шахматах №7: Сквозная атака на фигуру соперника
Потренируйтесь находить эти ключевые элементы в разных позициях, и вы заметите, что начнете выигрывать в шахматы часто!
6. Всегда держите все ваши фигуры под защитой
Игроки-любители игнорируют данное важное правило и расплачиваются за это. Даже если вам в моменте кажется достаточно безопасным оставить своего коня без защиты, дважды подумайте, прежде чем это сделать (хотя есть исключения).
В шахматах все быстро развивается, и очень легко пропустить тактический удар. Одна из популярных стратегий включает в себя комбинацию из нескольких шахов с последующим двойным ударом на незащищённые фигуры. В таком случае их невозможно защитить все одновременно, и одну в конечном счёте придется потерять.

Выигрышная стратегия в шахматах №8: Сохраняйте свои фигуры под защитой
7. Сохраните свою пешечную структуру в наилучшем виде
Многие игроки полагают, что пешечная структура играет важную роль только в гроссмейстерских играх. Это не так. Если ваша пешечная структура слаба, даже на уровне ниже 1800 вы окажетесь в невыгодном положении. Слабые, изолированные или сдвоенные пешки не могут защитить себя и требуют постоянной защиты от других фигур. Если пешки недостаточно защищены, они упадут.
И все мы знаем, что очень трудно выиграть в шахматы, если у вас не хватает 2-3 «солдат» в Пешечном окончании.
Чтобы избежать этого печального сценария, всегда учитывайте изменение пешечной структуры, когда вы:
- размениваете пешки
- продвигаете пешки
- размениваете фигуры
Здоровая пешечная структура — огромный плюс не только в эндшпиле, но и в миттельшпиле. Не имея очевидных слабостей, вы значительно усложните задачу вашему оппоненту по компрометации вашей позиции.
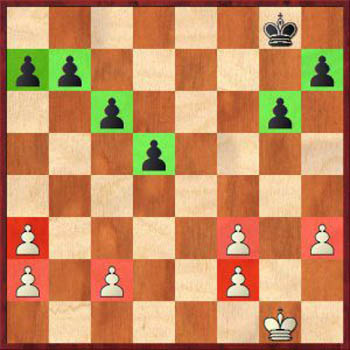
Выигрышная стратегия в шахматах №9: Держите свою пешечную структуру в хорошей форме
8. Всегда ищите возможности для атаки
Одна из распространенных ошибок клубных игроков — они пассивны и не ищут возможности атаковать. Даже если вы защищаетесь, всегда параллельно идите в контратаку. Гораздо сложнее победить игрока, который не только защищается, но и делает активные ходы, доставляя неприятности противнику.
Вы должны выработать привычку спрашивать себя после каждого хода «где я могу атаковать» и «каковы слабые стороны позиции противника»? Если хотите победить, вы должны научиться запускать и проводить атаки. Да, это непросто, но с практикой станет легче.
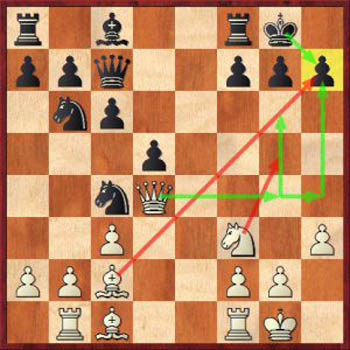
Выигрышная стратегия в шахматах № 10: Атака, атака, атака!
9. Если вы играете чёрными, это не значит, что вы в невыгодном положении
Многие клубные игроки думают, что если им выпало быть на чёрной стороне, то придётся играть на уравнивание или другими словами, на ничью. Это утверждение отчасти верно для профессиональных шахмат. Однако в шахматах до 2000 ЭЛО игра чёрными не означает автоматически более слабые позиции.
Большинство исходов партий на этом уровне определяются не крошечными преимуществами, полученными в дебюте. Большее значение имеет разница в материале, серьезные и позиционные ошибки. Если ваш рейтинг не превышает 2200, то не беспокойтесь о цвете фигур. У вас абсолютно равные шансы на победу.

Выигрышная стратегия в шахматах № 11: Чёрными фигурами нужно играть на победу
10. Научитесь играть форсированные ходы
Форсированные ходы заставляют вашего противника реагировать на них. Например, если вы ставите шах королю, то ваш соперник обязан выйти из-под шаха. Таким образом, шах является форсированным ходом. Если вы захватите фигуру противника, то ему, скорее всего, нужно будет отбить её обратно. И это также форсированный ход.
Почему в шахматах важны форсированные ходы?
Форсированные ходы упрощают процесс расчёта, следовательно, снижают неопределенность в игре. Если вы видите, как можете поставить мат противнику через постоянные шахи королю, то это будет намного безопаснее, чем если бы ваша комбинация не предполагала форсированных ходов. Гораздо легче держать ситуацию под контролем, когда вам нужно рассчитать лишь один вариант. Поэтому, если вы хотите выигрывать в шахматы, вам нужно научиться определять форсирующие ходы и применять их в своих играх.
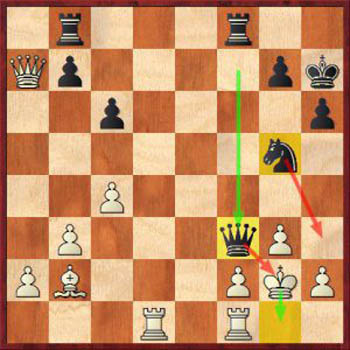
Выигрышная стратегия в шахматах № 12: Применяйте форсированные ходы
Поздравляем — теперь вы знаете, как регулярно выигрывать в шахматы!
Примечание: Если вы стремитесь к резкому увеличению шахматного уровня , то необходимо систематически работать над всеми элементами игры:
- Тактика
- Позиционная игра
- Атакующие навыки
- Техника эндшпиля
- Анализ классических игр
- Психологическая подготовка
- И еще многое другое
На первый взгляд кажется, что предстоит много работы. Но благодаря нашему учебному курсу Ваше обучение пройдёт легко , эффективно и с минимальными затратами времени. Присоединяйтесь к программе обучения «Шахматы. Перезагрузка за 21 День», прямо сейчас!
Источник: xchess.ru
