Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использованию статистических данных для научных и практических выводов. При этом статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками.
Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой. Число объектов N из генеральной совокупности и из выборки n называются соответственно объемом генеральной совокупности N и объемом выборки n.
Статистическое описание и вероятностные модели применяются к физическим, экономическим, социологическим, биологическим процессам, обладающим тем свойством, что хотя результат отдельного измерения физической величины X не может быть предсказан с достаточной точностью, но значение некоторой функции от множества результатов повторных измерений может быть предсказан с существенно лучшей точностью. Такая функция называется статистикой. Часто точность предсказания некоторой статистики возрастает с возрастанием объема выборки.
Элементы статистики. Дисперсия. Стандартное отклонение
Наиболее известные статистики – относительная частота, выборочные средние, дисперсия. Когда возрастает объем выборки n, многие выборочные статистики сходятся по вероятности к соответствующим параметрам теоретического распределения величины X. Поэтому каждую выборку рассматривают как выборку из теоретически бесконечной генеральной совокупности, распределение признака в которой совпадает с теоретическим распределением вероятности случайной величины. Во многих случаях теоретическая генеральная совокупность есть идеализация действительной совокупности, из которой получена выборка.
Различные значения наблюдаемого признака, встречающегося в совокупности, называются вариантами. Частоты вариантов выражают доли (удельные веса) элементов совокупности с одинаковыми значениями признака. Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующим им частотами.

Средние значения выборки
Значения, находящиеся в середине вариационного ряда, принято делить на собственно средние и структурные средние. Собственно среднее — это арифметическое среднее. Структурные средние — мода и медиана. Кроме того, чтобы охарактеризовать структуру вариационного ряда, используют квартили, квинтили, децили и процентили. Теперь обо всём по порядку.
Среднее арифметическое значение генеральной совокупности находят по формуле:
— число единиц генеральной совокупности,
— значение j-го наблюдения.
Если величина выборки X может принимать значения с вероятностями соответственно , то средним значением величины X для выборки (её математическим ожиданием E(x) ,будет
или
или же (2)
для негруппированных выборок и
для группированных выборок, где
— число единиц выборки,
— число классов,
— значение i-го класса,
— частота i-го класса.
Пример 1. В таблице даны значения средней температуры воздуха в населённом пункте N в 2014 году:
| Месяц | |
| 1 | -2,3 |
| 2 | -4,0 |
| 3 | 2,0 |
| 4 | 9,0 |
| 5 | 10,0 |
| 6 | 19,4 |
| 7 | 19,9 |
| 8 | 17,1 |
| 9 | 14,9 |
| 10 | 7,3 |
| 11 | 2,2 |
| 12 | -0,3 |
Найти среднюю температуру воздуха.
Решение. Найдём среднюю температуру воздуха как среднее значение для негруппированной выборки:
Пример 2. В таблице – данные о группировке сельских хозяйств по урожайности зерновых:
Урожайность зерновых в центнерах с га
Число сельских хозяйств – абсолютное
Удельный вес сельских хозяйств – в процентах
Источник: function-x.ru
Генеральная и выборочная дисперсии.
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят следующую характеристику — генеральную дисперсию.
Генеральной дисперсией Dr называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней хг.
Если все значения x1 х2. xNпризнака генеральной совокупности объема N различны, то

Если же значения признака хг, х2. xk имеют соответственно частоты N1, N2 … Nk причем ni + N2 +. + Nk = N, то

| xi | 2 | 4 | 5 | 6 |
| Ni | 8 | 9 | 10 | 3 |
Задание 8-5. Найти генеральную дисперсию для генеральной совокупности, заданной таблицей распределения:


Генеральным средним квадратическим отклонением (стандартом) называется s =
Найдем дисперсию признака X, рассматриваемого как случайную величину:




Таким образом, дисперсия D (X) равна Dr.
Такой же итог следует, если значения x1 х2. xkимеют соответственно частоты N1t N2,. » Nk.
В случае непрерывного распределения признака X по определению полагают:


Эту формулу можно записать в виде:



Величина называется средней квадратической ошибкой.
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего значения вводят выборочную дисперсию.
Выборочной дисперсией DB называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней .
Если все значения x1 x2,. хп признака выборки объема п различны, то

Если же значения признака x1 x2,. хk имеют соответственно частоты n1 n2…nk, причем n1 +n2+…+nk,= n, то
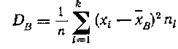

Выборочным средним квадратическим отклонением (стандартным отклонением) называется квадратный корень из выборочной дисперсии:
| xi |
| nt |
Задание 8-6. Выборочная совокупность задана таблицей распределения. Найти выборочную дисперсию



Не уменьшая общности рассуждений, будем считать значения x1 x2, … хп признака различными.
Выборочную дисперсию, рассматриваемую как случайную величину, можно обозначать Ŝ 2 :



Теорема. МО выборочной дисперсии равно или
Если варианты xj — большие числа, то для облегчения вычисления выборочной дисперсии DB в фо рмулу вводится ложный нуль C:

Задание 8-7. Для данных задания 8-4 вычислить выборочную дисперсию, ложный нуль оставить равный C = 72,00




3.3. Оценки параметров распределения.
Одной из задач статистики является оценка параметров распределения случайной величины X по данным выборки. Это значит, что по результатам, полученным по некоторой выборке данной совокупности, требуется сделать обобщение, которое распространяется на всю рассматриваемую выборку. Естественно такое обобщение будет не точным.
Выборочная дисперсия Dв считается смещенной оценкой генеральной дисперсии Dг. При этом ведется речь об исправлении выборочной дисперсии так. что бы ее математическое ожидание было равно генеральной дисперсии.
Исправленную дисперсию, как правило, обозначают S 2 . Доказано, что зависимость между выборочной и генеральной дисперсией находится в следующей зависимости:
Отметим, что если варианты х, — большие числа, то для облегчения вычисления s 2 формулу для s 2 аналогично преобразуют к виду:

где С — ложный нуль.
Выборочное среднее квадратичное s считается также смещенным, что бы оно стало исправленным надо воспользоваться соотношением:
В теоретических рассуждениях считают, что генеральная совокупность бесконечна. Для оценки параметров распределения X из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров.
Можно сразу вычислять исправленную дисперсию, если в формуле для вычисления выборочной дисперсии сумму квадратов отклонений делить не на число n, на число n-1.

Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки, для того чтобы не делать систематической ошибки в сторону завышения или занижения.
Ясно, что, чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной. Оценка, обладающая таким свойством, называется эффективной.
Кроме понятия «смещенные оценки», часто рассматривают такое понятие как «состоятельность оценки».
Состоятельной оценкой называют такую оценку Ŵ параметра W, что для любого, заданного числа ε > 0, вероятность P(Ŵn-W)< ε.
Впрочем, любая оценка, предназначенная для практического применения должна быть состоятельной оценкой.
Задание 8-8. С плодового дерева случайным образом отобрано 10 плодов. Их веса (в граммах) записаны в первой колонке приведенной таблицы. Обработать статистические данные выборки.
Решение. Для вычисления хв и s по формулам введем ложный нуль С = 250 и все необходимые при этом вычисления сведем в расчетную таблицу:





Отсюда:
Ответ. Генеральная средняя оценка веса плода равна 243 г со средней квадратической ошибкой в 9 г.
Оценка генерального среднего квадратического отклонения веса плода равна 28 г.
Источник: infopedia.su
Как найти дисперсию?
Дисперсия — это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая — значения сравнительно близки друг к другу, если большая — далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии — среднеквадратическое отклонение $sigma(X)=sqrt$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: «Дисперсия — это второй центральный момент случайной величины» (напомним, что первый начальный момент — это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
- Формула дисперсии случайной величины
- Примеры вычисления дисперсии
- Онлайн калькулятор для дисперсии
- Видео. Полезные ссылки
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле: $$ D(X)=M(X-M(X))^2, $$ которую также часто записывают в более удобном для расчетов виде: $$ D(X)=M(X^2)-(M(X))^2. $$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид: $$ D(X)=sum_^-left(sum_^ right)^2. $$ Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом: $$ D(X)=int_<-infty>^ <+infty>f(x) cdot x^2 dx — left( int_<-infty>^ <+infty>f(x) cdot x dx right)^2. $$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения: $$ x_i quad 1 quad 2 \ p_i quad 0.5 quad 0.5 $$ и $$ y_i quad -10 quad 10 \ p_i quad 0.5 quad 0.5 $$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором — дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии: $$ D(X)=sum_^-left(sum_^ right)^2 =\ = 1^2cdot 0.5 + 2^2 cdot 0.5 — (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25. $$ $$ D(Y)=sum_^-left(sum_^ right)^2 =\ = (-10)^2cdot 0.5 + 10^2 cdot 0.5 — (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100. $$ Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором — на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения: $$ x_i quad -1 quad 2 quad 5 quad 10 quad 20 \ p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1 $$
Снова используем формулу для дисперсии дискретной случайной величины: $$ D(X)=M(X^2)-(M(X))^2. $$ В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание: $$ M(X)=sum_^ =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8. $$ Потом математическое ожидание квадрата случайной величины: $$ M(X^2)=sum_^ = (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4. $$ А потом подставим все в формулу для дисперсии: $$ D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16. $$ Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины: $$ D(X)=int_<-infty>^ <+infty>f(x) cdot x^2 dx — left( int_<-infty>^ <+infty>f(x) cdot x dx right)^2. $$ Вычислим сначала математическое ожидание: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx = int_^ frac cdot x dx = int_^ frac dx = left.frac right|_0^6=frac = 4. $$ Теперь вычислим $$ M(X^2)=int_<-infty>^ <+infty>f(x) cdot x^2 dx = int_^ frac cdot x^2 dx = int_^ frac dx = left.frac right|_0^6=frac = 18. $$ Подставляем: $$ D(X)=M(X^2)-(M(X))^2=18-4^2=2. $$ Дисперсия равна 2.
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Полезная страница? Сохрани или расскажи друзьям
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения. Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по ТВ. Для закрепления материала — еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Источник: www.matburo.ru
