548 дней сколько месяцев

Примечание: данный пост является переводом статьи cmcenroe.me/2014/12/05/days-in-month-formula.html (Часть I), а также авторским к нему дополнением (Часть II). Не следует относиться к материалу серьёзно, а скорее как к разминке для ума, требующей не более чем школьных знаний арифметики и не имеющей практического применения. Всем приятного чтения!

Часть I

Вступление

Недавно, после очередной бессонной ночи, я размышлял о методах запоминания количества дней в каждом месяце года. Для этого есть считалочка, а также способ считать на костяшках пальцев, но ни то, ни другое меня не устроило. Я задумался, а не существует ли какой-нибудь математической формулы для решения такой задачи, и — не обнаружив при беглом изучении таковую — бросил себе вызов её создать.

ФормализуяДругими словами, необходимо найти функцию f, такую, что значение f(x) для каждого месяца x, представленного числом от 1 до 12, равняется количеству дней в этом месяце. Таблица значений аргумента и функции 1 :

Сколько месяцев в году имеют 28 дней

x f(x)

1	2	3	4	5	6	7	8	9	10	11	12
31	28	31	30	31	30	31	31	30	31	30	31

Если у вас возникло желание попробовать самому до прочтения моего решения, то сейчас самое время. Если же вы предпочитаете немедленно увидеть готовый ответ, то посмотрите под спойлер.

Ниже следуют мои шаги по нахождению решения.

Математический аппарат

Сначала бегло освежим в памяти два жизненно необходимых в решении этой задачи оператора: целочисленное деление и остаток от деления.

Целочисленное деление это оператор, применяемый во многих языках программирования при делении двух целых чисел и отбрасывающий от частного дробную часть. Я буду изображать его как . Например:

Остаток от деления это оператор, находящий остаток от деления. Во многих языках программирования применяется символ %, я же буду использовать конструкции вида , например:

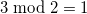
Замечу, что остаток от деления имеет равный с делением приоритет.

Основы

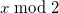
Итак, применим наш математический аппарат для получения базовой формулы. 2 В обычном месяце 30 или 31 день, так что мы можем использовать для получения поочерёдно 1 или 0, а затем просто прибавить к этому числу константу:

Паша Техник вопросы для тупых

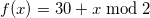
Получаем таблицу, полужирным выделены корректные значения:

x f(x)

1	2	3	4	5	6	7	8	9	10	11	12
31	30	31	30	31	30	31	30	31	30	31	30

Неплохое начало! Уже есть правильные значения для января и для месяцев с марта по июль включительно. Февраль — особый случай, и с ним мы разберёмся чуть позже. После июля для оставшихся месяцев порядок получения 0 и 1 должен быть изменён на обратный.
Для этого мы может прибавить к делимому 1:

x f(x)

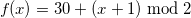
1	2	3	4	5	6	7	8	9	10	11	12
30	31	30	31	30	31	30	31	30	31	30	31

Теперь правильные значения с августа по декабрь, но, как и предполагалось, значения для прочих месяцев неверны. Давайте посмотрим как мы можем объединить эти формулы.

Наложение маски

Для этого необходима кусочно-заданная функция, но — так как мне это показалось скучным — я задумался о другом пути решения, использующем одну часть функции на одном интервале, другую — на другом.
Полагаю, что проще всего будет найти выражение, равное 1 в одной области применения и 0 — в остальной. Метод, в котором умножая аргумент на выражение мы исключаем его из формулы вне области его применения, я назвал «наложением маски», потому такое поведение подобно некой битовой маске.
Для применения этого метода в последней части нашей функции необходимо найти выражение, равное 1 при , и — так как значения аргумента всегда меньше 16 — для этого прекрасно подходит целочисленное деление на 8.

x ⌊ x ⁄8⌋

1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	0	0	0	0	1	1	1	1	1

Теперь с помощью этой маски, используя в делимом выражение вместо 1, мы можем заменить порядок получения 0 и 1 формуле на обратный:

x f(x)

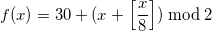
1	2	3	4	5	6	7	8	9	10	11	12
31	30	31	30	31	30	31	31	30	31	30	31

Эврика! Всё правильно, кроме февраля. Сюрприз-сюрприз.

Февраль

В любом месяце 30 или 31 день, кроме февраля с его 28 (високосный год выходит за рамки этой задачи). 3 На текущий момент по нашей формуле в нём 30 дней, поэтому неплохо бы вычесть выражение, равное 2 при

.
Лучшее что мне удалось придумать это , что накладывает маску на все месяцы после февраля:

x 2 mod x

1	2	3	4	5	6	7	8	9	10	11	12
0	0	2	2	2	2	2	2	2	2	2	2

Изменив базовую константу на 28 с добавлением 2 к остальным месяцам получим формулу:

x f(x)

1	2	3	4	5	6	7	8	9	10	11	12
29	28	31	30	31	30	31	31	30	31	30	31

К сожалению, январь теперь короче на 2 дня. Но, к счастью, получить выражение, которое будет применяться только для первого месяца очень легко: это округлённое вниз обратное к

число. Умножив его на 2 получаем окончательную формулу:

x f(x)

1	2	3	4	5	6	7	8	9	10	11	12
31	28	31	30	31	30	31	31	30	31	30	31

Послесловие

Вот она — формула для получения количества дней в любом месяце года, использующая простейшую арифметику. В следующий раз когда вы будете вспоминать сколько же дней в сентябре, просто выполните с помощью этой однострочной функции на JavaScript:

function f(x) < return 28 + (x + Math.floor(x/8)) % 2 + 2 % x + 2 * Math.floor(1/x); >

Часть II

Вступление

В первой части была получена короткая и даже немного изящная формула, основными достоинствами которой являются простота математического аппарата, отсутствие ветвлений и условных выражений, лаконичность. К недостаткам — кроме того, что вы не будете применять её в вашем проекте — можно отнести отсутствие проверки на вискокосный и не високосный год.
Поэтому я поставил перед собой задачу создать функцию f, такую, что значение f(x, y) для каждого месяца x, представленного числом от 1 до 12 и года y, большего 0, равняется количеству дней в месяце x в году y.
Для нетерпеливых под спойлером находится готовый ответ, остальных же прошу следовать за мной.

Остаток от деления: mod и ⌊⌋

Для визуальной наглядности договоримся, что в некоторых формулах оператор деления с остатком заменён нижними скобками, там где это показалось мне необходимым:

Високосный год

В високосный год вводится дополнительный день календаря: 29 февраля. Как известно, високосным является год, кратный 4 и не кратный 100, либо кратный 400. Запишем тождественное этому высказыванию выражение:

Для приведения этого выражения в алгебраическое, необходимо применить к результату выражения инъекцию вида:

Что позволит получить 1 при делении без остатка и 0 при делении с остатком, чтобы использовать её в формуле определения количества дней в месяце.

В качестве функции g’ можно использовать 1 минус остаток от деления для :

x g'(x)

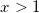0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Infinity	1	0	0	0	0	0	0	0	0	0	0	0	0	0

Легко заметить, что увеличив делимое и делитель на 1 мы получим правильную формулу при :

x g'(x)

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Таким образом выражение запишем как:

А выражение запишем как:

Применяя этот подход получим следующую функцию g(y), значением которой будет 1, если год високосный, или 0 в обратном случае:

y g(y) y g(y)

1990	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000
0	0	1	0	0	0	1	0	0	0	1
2000	2100	2200	2300	2400	2500	2600	2700	2800	2900	3000
1	0	0	0	1	0	0	0	1	0	0

Полужирным выделены високосные года.

Напоминаю, что в рамках принятой договорённости оператор получения остатка от деления может быть изображен как mod, так и ⌊⌋.

Наложение маски

В формуле часть является поправкой, прибавляющей 2 дня к январю. Если убрать множитель 2 и в числителе заменить 1 на 2, тогда эта формула будет прибавлять 2 дня к январю и 1 день к февралю, что даёт нам ключ к добавлению дня в високосном году. Для наглядности используем в формуле промежуточное значение g(y) и в качестве y используем 2000 (високосный) и 2001 (не високосный) годы:

x f(x, 2000) f(x, 2001)

1	2	3	4	5	6	7	8	9	10	11	12
31	29	31	30	31	30	31	31	30	31	30	31
30	28	31	30	31	30	31	31	30	31	30	30

Значения для всех месяцев, кроме января не високосного года верны.

Для исправления этого досадного недоразумения добавим к январю 1 день уже известной нам формулой :

x f(x, 2000) f(x, 2001)

1	2	3	4	5	6	7	8	9	10	11	12
32	29	31	30	31	30	31	31	30	31	30	31
31	28	31	30	31	30	31	31	30	31	30	30

Теперь необходимо вычесть 1 день из января в случае високосного года, для чего нам поможет знание того, что для любого x 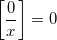, а .

Тогда формула примет вид:

x f(x, 2000) f(x, 2001)

1	2	3	4	5	6	7	8	9	10	11	12
31	29	31	30	31	30	31	31	30	31	30	31
31	28	31	30	31	30	31	31	30	31	30	30

Заключение

В результате получена уже значительно более громоздкая, но более универсальная формула, которую также можно использовать для получения количества дней в месяце определённого года:

function f(x, y) < return 28 + ((x + Math.floor(x / 8)) % 2) + 2 % x + Math.floor((1 + (1 — (y % 4 + 2) % (y % 4 + 1)) * ((y % 100 + 2) % (y % 100 + 1)) + (1 — (y % 400 + 2) % (y % 400 + 1))) / x) + Math.floor(1/x) — Math.floor(((1 — (y % 4 + 2) % (y % 4 + 1)) * ((y % 100 + 2) % (y % 100 + 1)) + (1 — (y % 400 + 2) % (y % 400 + 1)))/x); >

Пример на C# ideone.com/fANutz.

1. Я не умею пользоваться подобной мнемоникой, поэтому подсмотрел табличку в интернете.
2. «Основы», или «Правило С Многими Исключениями», как и большинство правил.
3. Изначально в римском календаре февраль был последним месяцем года, поэтому есть логика в том, что он короче всех остальных. Также есть логика в добавлении или удалении дня именно в конце года, поэтому его длина является переменной.

Upd. 1:
Альтернативный перевод первой части в сообществе вконтакте.
Upd. 2: Благодаря комментарию keksmen исправлена ошибка в формуле определения високосного года (g(y)) и исправлена итоговая формула.

• занимательная математика
• никто не читает тэги
• юмор

Источник: habr.com

Калькулятор календарных дней между датами

Расчет календарных дней между датами — задача не сложная, но требующая времени и внимательности, особенно если речь идет о длительном периоде времени. Простая арифметика при данных расчетах поможет мало в виду того, что в месяцах разное количество дней, года бывают високосные, а при некоторых расчетах приходится также опускать выходные и праздничные дни.

Калькулятор календарных дней между датами выполнит эту задачу легко и безошибочно.

Работа с калькулятором

Калькулятор избавит пользователя от необходимости подсчета дат путем подчеркивания цифр в календаре и последующего сложения черточек. Достаточно ввести в окно калькулятора даты, ограничивающие промежуток времени и получить искомую цифру мгновенно.

Алгоритмы работы калькулятора подчинены требованиям ст. 15 Закона РФ «О бухгалтерском учете», которая устанавливает правила расчета по календарным датам.

Работа бухгалтера, как никакая другая, связана с подсчетом дней, будь то исчисление периода промежуточной отчетности или подсчет рабочих дней.

Назначение калькулятора, в первую очередь, это облегчение труда бухгалтера и сокращение затрат его времени на несложные, но нудные подсчеты.

Несомненно, полезным будет калькулятор и в работе юристов, которая также тесно связана с датами — сроками исковой давности (особенно в случае их прерывания), сроками подачи апелляционных жалоб, сроками погашения судимости, сроками предъявлений претензий, вычислениями времени вынужденного прогула и т.д.

Применительно к гражданскому праву калькулятор календарных дней между датами работает также и с учетом положений ст. 193 ГК РФ. Вообще практически все процессуальные кодексы в той или иной мере регламентируют исчисление сроков по календарным дням применительно к регламентируемым ими правоотношениям.

В договорном праве, к примеру, сроки являются существенными условиями договора. Соответственно, правильное исчисление сроков является существенным условием добросовестного исполнения договорных условий.

Для того, чтобы получить интересующий вас результат, в верхнее окно калькулятора введите начальную дату, от которой будет произведен расчет. В нижнее окно введите конечную дату, то есть дату прекращения расчета. При необходимости поставьте галочку в случае, если последний день должен быть включен в расчет.

Источник: assistentus.ru

Андрей Воробьев и его конкуренты. Рассказываем, что известно о кандидатах в губернаторы Подмосковья

Выбора губернатора Московской области начались 8 сентября и продлятся до 10 числа. Главу региона жители будут выбирать на ближайшие пять лет.

Нынешний губернатор Андрей Воробьев взошел на пост в ноябре 2012 года и в этот раз снова выдвинул свою кандидатуру. С ним будут соперничать еще три кандидата. Мы решили вспомнить, кто именно претендует на должность главы Подмосковья и чем известны эти люди. Рассказываем, кто может стать следующим губернатором Московской области.

Андрей Воробьев («Единая Россия»)

Нынешний глава региона родился в Красноярске в 1970 году. Его отец — Юрий Воробьев — бывший заместитель главы МЧС России, которым на тот момент был Сергей Шойгу. С 2008 года Воробьев-старший является зампредом Совета Федерации РФ.

В детстве Воробьев занимался хоккеем и играл за сборную Красноярского края. В школе он любил изучать гуманитарные предметы, особенно литературу и русский язык.

После школы он ушел в армию, а позднее окончил Северо-Осетинский государственный университет по специальности «коммерция» и экономический факультет Академии внешней торговли. В 1988–1990 годах он служил в армии и принимал участие в операциях в Баку, Ереване, Коканде и Фергане.

В конце девяностых Воробьев занимался рыбным бизнесом: он был генеральным директором ЗАО «Русская рыбная компания», а также группы компаний «Русское море». Позднее он продал акции своему брату Максиму.

В начале нулевых годов Воробьев попал в Госдуму: он был членом комитета по образованию и науке, позднее — комитета по делам общественных объединений и религиозных организаций. Кроме того, с 2005 по 2012 год Воробьев руководил ЦИК ВПП «Единая Россия», пока в феврале 2012 года внезапно не сообщил, что покидает пост, чтобы сосредоточиться на работе в Госдуме.

Губернатором Московской области он стал после череды перестановок: Шойгу, который руководил регионом всего полгода, назначили министром обороны, и через два дня после этого лично Путин назначил Воробьева на должность врио главы области. В сентябре 2013 года его избрали губернатором на выборах с 78,94% голосов, в сентябре 2018 года — переизбрали с 62,52% голосов избирателей.

Александр Наумов (КПРФ)

Александр Наумов родился в Москве в 1964 году. В 1986-м он окончил Московский институт электронной техники по специальности «автоматизированные системы обработки информации и управления», после чего отслужил в армии.

Впоследствии Наумов занимался продажей программного обеспечения и компьютерной техники, пока в 1999 году не вступил в партию «КПРФ». Через четыре года он стал депутатом Госдумы и регулярно переизбирался, войдя в ее пятый, шестой и седьмой созывы. В 2020 году Наумов стал депутатом Мособлдумы и возглавил фракцию КПРФ.

В своей программе он выступает за поддержку малого и среднего бизнеса, решение экологических проблем и развитие агропромышленного комплекса.

Кирилл Жигарев (ЛДПР)

Жигарев — самый молодой кандидат на место губернатора Московской области. Он родился в 1988 году в столице. Его политическая карьера началась достаточно рано, в 23 года, сразу после окончания МГУ.

Его отец — Сергей Жигарев — депутат двух созывов Госдумы от ЛДПР, впоследствии — депутат Мособлдумы от «Справедливой России».

Первые два года Кирилл Жигарев работал в администрациях сельских поселений Наро-Фоминского района, а в 2011 году был избран депутатом Мособлдумы по партийному списку, и переизбран туда же в 2016 году.

Ранее он уже участвовал в выборах губернатора, но безуспешно: в 2018 году Жигарев набрал 5,8% голосов и занял четвертое место.

В своей предвыборной программе он делает упор на традиции и «русскую идентичность», а также развитие медицины и поддержку местного самоуправления.

Анатолий Никитин («Справедливая Россия»)

Никитин родился в 1975 году в Москве, но постоянно живет в подмосковной Коломне. С молодого возраста он занимался бизнесом: в 1996 году предприниматель вместе со своим отцом основал НПО «СОМЭКС». Компания занимается производством оборудования для добычи полезных ископаемых.

В 1998 году Никитин окончил РЭА имени Плеханова по специальности «инженер-механик», а в 2002 году получил кандидатскую степень по экономике. В Мосгордуму он попал относительно недавно: в 2021 году. Также он является членом Общероссийского отраслевого объединения работодателей «Союз машиностроителей России».

Союз машиностроителей России создали в 2007 году для «представления интересов российских машиностроительных предприятий». Союз формирует стратегию развития отрасли и занимается поддержкой профильного комплекса.

В своей предвыборной кампании Никитин заявляет, что ставит в приоритеты «интересы простых граждан» и развитие предпринимательства в Подмосковье.

10 сентября 2023 года выборы пройдут и в столице. Мы подробно рассказывали, кто будет бороться за пост мэра Москвы.

Источник: msk1.ru